Atividade 1 - 4º Bimestre –
Professor Carlos Ribeiro Cardoso - 8ºC
4.5
SEQUÊNCIA DIDÁTICA – GEOMETRIA Habilidade - EF08MA18
(EF08MA18)
Reconhecer e construir figuras obtidas por composições de transformações
geométricas (translação, reflexão e rotação), com o uso de instrumentos
de desenho ou de softwares de geometria dinâmica.
1-No quadro abaixo podemos observar 3
tipos diferentes de transformações geométricas:
a)
b)
c)
Associe
corretamente a letra correspondente ao movimento:
( ) Rotação
( ) Translação
( ) Reflexão
2-Qual das seguintes figuras não
representa uma transformação geométrica de reflexão?
A)
B)
C)
D)
3-Desenhe a reflexão dessa imagem em relação à linha:
4-A partir da figura abaixo,
utilizando régua, lápis de escrever e lápis de cor execute as
transformações:
a) Rotação de 90°:
b) Reflexão vertical:
c) Translação na diagonal:
Fonte pesquisa:
https://novaescola.org.br/plano-de-aula/1646/simetria-de-translacao-rotacao-e-reflexao#materiais-e-atividades
Para finalizar
Realizar os exercícios da apostila volume 4
matemática 8º Ano
Pg 103 até pg 116
Atividades 1 até atividade 6
Atividade 2 - 4º Bimestre
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
O litro (l) e o metro cúbico (m³) são duas unidades de medidas fundamentais quando se trata de capacidade e volume, respectivamente. Mas, em muitas ocasiões, este volume ou esta capacidade não são apresentadas nestas unidades, e então recorremos a seus múltiplos ou submúltiplos. Na tabela, a seguir, são apresentados os submúltiplos dessas duas unidades de medida:
Usando a relação 1 m3 = 1000 l, determine em litros qual é a capacidade que corresponde a cada um deles.
a) 4,5 m3 = 4,5 x 1000 = 4 500 litros
b) 530 dm3 = 530 x 1= 1 litro
c) 9 400 cm3 = 9400 : 1000 = 9,4 litros
d) 4 cm3 = 4 : 1000 = 0,004 litros
e) 15 dm3 = 15 x 1 = 15 litros
Exercício 1 - Converta em litros
a) 5,7 m³ =
b)578 dm³ =
c)3 490 cm³ =
d) 7 cm³ =
e) 278dm³ =
Exercício 2 -
Observação (1 litro = 1000ml)
1-Eduardo comprou uma caixa de refrigerantes com 12 latinhas de 350ml. Ele disse a Kely que beberia tudo de uma única vez. Kely então disse que se ele bebesse apenas 3 litros de refrigerante ela já o chamaria de maior bebedor de refrigerante do bairro. Será que uma caixa de refrigerante será suficiente para Eduardo ganhar esse título?
2-Kely sabendo do resultado, disse que se ele não conseguisse, levaria
todo o restante para a sua casa. Ocorre que Eduardo só tomou 2
latinhas. Quantos litros de refrigerante sobraram para Kely levar para
sua casa?
3-Kely ficou com o sorriso de orelha a orelha. Então, Eduardo,
para não ficar tão para trás, desafiou Kely a beber mais
refrigerante do que ele. Ela bebeu e no fim contabilizou
1,5litros. Quantas latinhas aproximadamente este
valor representa?
4-Jonas fez um reservatório extra para água em sua casa, que tem
um formato cúbico com arestas de 1 metro. Sabendo que ele já
colocou 250 litros de água e essa quantidade preencheu ¼ desse
reservatório, calcule o volume desse reservatório
(em metros cúbicos) e quantos litros de água serão
necessários para encher esse reservatório.
5-Juliana faz queijos para vender e comprou um coalho de marca
nova, porém a embalagem traz medidas diferentes das
que ela utiliza normalmente. O rótulo diz o seguinte: utilizar
5 cm3 de coalho em 10dm3 de leite. Quais são as quantidades
em mililitros de coalho que Juliana tem que utilizar para
30 litros de leite?
6-Uma caixa d’água com capacidade 60 m3 reserva
água para abastecer um bairro da cidade. Quantos
reservatórios de 2.000 Litros essa caixa d’água
pode abastecer?
7-Elabore um problema que envolva a conversão
de valores de volume de um recipiente. Em
seguida compartilhe com a turma sua criação.
Exercício 3
Observação ( Volume = comprimento X largura X altura)
Unidades de medidas ( m³=metro cúbico - cm³ = centímetro cúbico - dm
1-A foto acima foi tirada por Dani. Ela mora em um apartamento
no centro da cidade de Lucas do Rio Verde, e lá dispõe de
uma piscina de formato retangular. Curiosa que é, olhou para
a placa de aviso e observou as medidas de dimensões da piscina,
e percebeu que o valor de sua capacidade estava apagado. Para
corrigir isso ela fez os cálculos e anotou a caneta o valor encontrado.
Sabendo que as medidas da piscina são 10m x 4m x 1,5m
indique a capacidade de água que ela detém.
2-Sabendo que 1m³ equivale a 1000 litros, encontre a medida
de volume que a piscina suporta.
3-Após fazer as contas, um garoto do apartamento
(que adora tomar tereré) brincou com Dani que um dia ainda
iria encher esta piscina de suco de limão para tomar com tereré.
Emendando a brincadeira, pegou uma lata de tinta vazia
(pois o prédio estava de reforma) que encontrou ali perto e
perguntou quantas latas destas cheias seriam então necessários
para encher a piscina, já que fariam o suco lata por lata até a
encher. Sabendo que as medidas da lata são 30cm x 30cm x 80cm
encontre o volume da lata.
4-Para encerrar a brincadeira, Dani desafiou o garoto a encher
a lata com a água da piscina e a esvaziar, para encontrar a
quantidade de latas que caberiam lá. O garoto por sua vez,
decidiu que seria mais inteligente mudar a unidade de
medida da lata (que está em cm³) para m³ e dividir o
volume encontrado na piscina pelo da lata para saber
quantas latas caberiam. Ciente deste trabalho, calcule
a quantidade de latas como o colega da Dani falou e
anote o valor encontrado:
5-Lucas quer colocar um novo enfeite em seu aquário
que tem 20cm de largura por 30 cm de comprimento e
30 cm de altura. Ele sabe que seu aquário está com 14
litros de água neste momento, e que em um teste
feito anteriormente ao colocar seu enfeite em
uma bacia com água ele deslocou 400 cm3 de l
íquido. Ele pode colocar esse enfeite em seu aquário
sem precisar retirar um pouco de água? Por quê?
6-Kátia tem em sua residência uma piscina cujo formato é um bloco
retangular de 2 x 4 x 1,60 m. Quando faz a limpeza da piscina
ela precisa repor a água em ⅙ do volume total da piscina.
Quantos litros de água ela vai repor na piscina?
7-Elabore um problema que envolva o cálculo do volume
de um recipiente com o formato de um bloco retangular.
Exercício 4 - Resolver a o exercício da apostila volume 4 - 8º ano
ATIVIDADE 2 – CÁLCULO DE VOLUMES: APLICAÇÕES PRÁTICAS
Página 117 - 2.1
pg118 - 2.2 ; 2.3 ;
pg119 - 2.4 : 2.5
Cilindro Reto
Em um cilindro, consideramos as seguintes áreas:
a) área lateral (AL)
Podemos observar a área lateral de um cilindro fazendo a sua planificação:
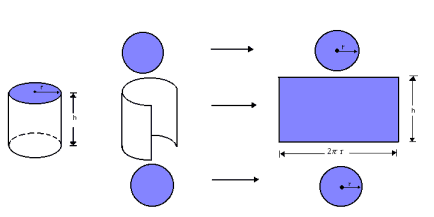
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões ![]() :
:
|
b) área da base (AB): área do círculo de raio r.
|
c) área total (AT): soma da área lateral com as áreas das bases.
|
Volume do cilindro
Para obter o volume do cilindro, vamos usar novamente o princípio de Cavalieri. Dados dois sólidos com mesma altura e um plano ![]() , se todo plano
, se todo plano ![]() , paralelo ao plano
, paralelo ao plano ![]() , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:
, intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:
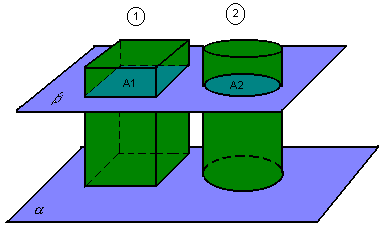
![]()
Se 1 é um paralelepípedo retângulo, então V2 = ABh. Assim, o volume de todo paralelepípedo retângulo e de todo cilindro é o produto da área da base pela medida de sua altura:
| Vcilindro = ABh |
No caso do cilindro circular reto, a área da base é a área do círculo de raio r: ![]() . Portanto, seu volume é:
. Portanto, seu volume é:
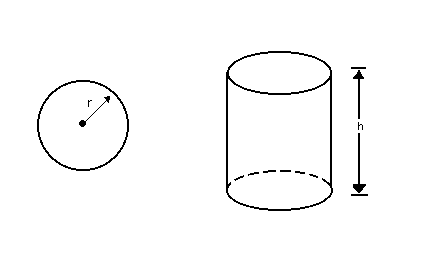
![]()
Fonte pesquisa:
https://www.somatematica.com.br/emedio/espacial/espacial16.php
Exemplo 1
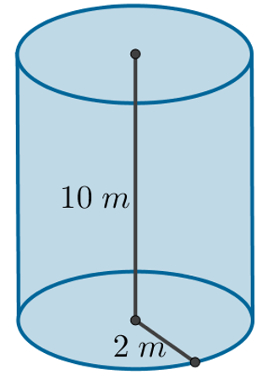
Um reservatório em formato cilíndrico possui raio igual a 2 metros e sua altura é de 10 metros, como mostra a imagem a seguir. Qual é o volume desse reservatório? (considere π = 3,14).
O volume do cilindro é dado pela área da base multiplicada por sua altura. Assim, podemos obter essa medida com a seguinte fórmula:
V = πr2·h
Substituindo os valores de π, do raio e da altura desse cilindro, teremos:
V = 3,14·22·10
V = 31,4·4
V = 125,6 m3
Fonte pesquisa:
https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-cilindro.htm
Resolver os exercícios da aposttila volume 4 - 8 º Ano
SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – CILINDROS RETOS
Pg119 - 1.1 e 1.2
Pg120 - 1.3 e 1.4
ATIVIDADE 2 – VOLUME DO CILINDRO RETO
Pg 120 - 2.1 e 2.2
Pg 121 - 2.3
SEQUÊNCIA DIDÁTICA – ESTATÍSTICA E PROBABILIDADE - Habilidade - EF08MA25
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
Mediana, Moda, Média e Média Ponderada
MATEMÁTICA
Moda, média e mediana são números que resumem as informações de uma lista de dados a apenas uma informação
Mediana
Se o conjunto de informações for numérico e estiver organizado em ordem crescente ou decrescente, a sua mediana será o número que ocupa a posição central da lista. Considere que a escola de música já citada possui nove professores e que suas idades são:
32 anos, 33 anos, 24 anos, 31 anos, 44 anos, 65 anos, 32 anos, 21 anos e 32 anos
Para encontrar a mediana das idades dos professores, devemos organizar a lista de idades em ordem crescente:
21, 24, 31, 32, 32, 32, 33, 44 e 65
Observe que o número 32 é o quinto. À sua direita, existem outras 4 idades, assim como à esquerda. Logo, 32 é a mediana da lista das idades dos professores.
21, 24, 31, 32, 32, 32, 33, 44, 65
Se a lista possuir um número par de informações, para encontrar a mediana (Ma), devemos encontrar os dois valores centrais (a1 e a2) da lista, somá-los e dividir o resultado por 2.
Ma = a1 + a2
2
Se as idades dos professores fossem 19 anos, 19 anos, 18 anos, 22 anos, 44 anos, 45 anos, 46 anos, 46 anos, 47 anos e 48 anos, a lista crescente com as duas medidas centrais seria:
18, 19, 19, 22, 44, 45, 46, 46, 47, 48
Observe que a quantidade de informações à direta e à esquerda desses dois números é exatamente a mesma. A mediana desse conjunto de dados é, portanto:
Ma = a1 + a2
2
Ma = 44 + 45
2
Ma = 89
2
Ma = 44,5 anos
Moda
É chamado de moda o dado mais frequente de um conjunto. Veja um exemplo:
Em uma escola de música, as turmas são formadas por apenas 8 alunos. Na turma “A”, estão matriculados Mateus, Mateus, Rodrigo, Carolina, Ana, Ana, Ana e Teresa.
Observe que há dois meninos chamados de Mateus e três meninas chamadas de Ana. O nome que mais se repete é Ana e, por isso, é a moda desse conjunto de dados.
Agora um exemplo com números: em uma escola de música, os oito alunos da turma “A” possuem as seguintes idades: 12 anos, 13 anos, 13 anos, 12 anos, 11 anos, 10 anos, 14 anos e 11 anos.
Perceba que as idades 11, 12 e 13 repetem-se o mesmo número de vezes e nenhuma idade aparece mais que essas três. Nesse caso, o conjunto possui três modas (11, 12 e 13) e é chamado de trimodal.
Também podem existir conjuntos bimodais, isto é, com duas modas; amodais, com nenhuma moda etc.
Média
Média (M), mais precisamente chamada de média aritmética simples, é o resultado da soma de todas as informações de um conjunto de dados dividida pelo número de informações que foram somadas. A média aritmética simples entre 14, 15 e 25, por exemplo, é a seguinte:
M = 14 + 15 + 25
3
Como há três dados na lista, dividimos a soma desses dados pelo número 3. O resultado é:
M = 54
3
M = 18
A média é a medida de centralidade mais usada por ser a que mescla de maneira mais uniforme os valores mais baixos e os mais altos de uma lista. No conjunto anterior, por exemplo, a mediana é igual a 44,5, mesmo com tantas idades próximas de 20 anos. Observe a média aritmética simples desse mesmo conjunto:
M = 18 + 19 + 19 + 22 + 44 + 45 + 46 + 46 + 47 + 48
10
M = 35,4 anos
Média ponderada
A Média Ponderada (Mp) é uma extensão da média simples e considera pesos para as informações do conjunto de dados. É feita por meio da soma do produto de uma informação pelo seu respectivo peso e, em seguida, a divisão desse resultado pela soma de todos os pesos usados.
Considere como exemplo os dados na tabela a seguir, que contém uma lista com as idades dos alunos do sexto ano da escola A. Vamos calcular a média das idades.
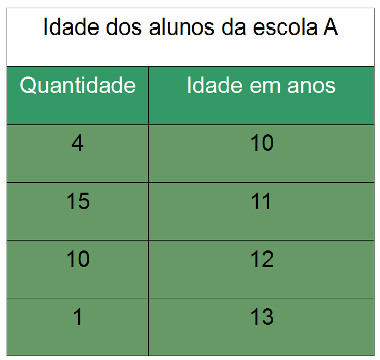
Existe a possibilidade de calcular a média simples ao somar 10 anos quatro vezes, 11 anos quinze vezes etc. Entretanto, por meio de uma média ponderada, podemos considerar a quantidade de alunos com 11 anos como o peso dessa idade nessa sala de aula; a quantidade de alunos que possuem 10 anos como peso dessa idade, e assim por diante até que todas as idades tenham sido somadas. Assim, o cálculo da média ponderada seria:
Mp = 4·10 + 15·11 + 10·12 + 1·13
4 + 15 + 10 + 1
Mp = 40 + 165 + 120 + 13
30
Mp = 338
30
Mp = 11,26 anos
Fonte : Por Luiz Paulo Moreira Graduado em Matemática
https://brasilescola.uol.com.br/matematica/moda-media-mediana.htm
Exercícios
1-No time de futebol que Marcelo joga há uma diferença de idade entre os jogadores. Ele decidiu anotar as idades dos jogadores para analisar se tinham algum padrão para poder entrar no time. Com isso calculou a média, mediana e moda e a partir das análises desses cálculos chegar a alguma conclusão.
a) Qual foi a média, mediana e moda encontrada por Marcelo?
b) Qual a conclusão que Marcelo chegou após os cálculos?
2-O gráfico a seguir apresenta o consumo de água, em metros cúbicos, da casa de Igor durante 5 meses.
a) Calcule a média, mediana e moda do consumo de água na casa de Igor.
b) Em relação aos valores encontrados da média e mediana, o que se pode concluir?
3-Em toda empresa há um sistema de ouvidoria, ou seja, uma Central de Atendimento para o registro de reclamações dos consumidores em relação aos serviços prestados. Esse atendimento é diário, por isso existe uma pessoa disponível para esse atendimento. Desse modo, a empresa que Pedro trabalha analisou a quantidade de ligações recebida durante uma semana, visando um melhor atendimento. Veja no quadro o número de reclamações.
a) Qual a média de reclamação da semana? E a mediana e a moda?
b) Quais os dias que as reclamações estão abaixo da média? Por que isso acontece?
c) Se a média, por semana, é de 17 ligações, que justificativa podemos dar para a moda encontrada?
d) É possível afirmar que a média está muito distante da realidade comparado com a mediana e a dispersão dos dados?
4-Foi realizado uma pesquisa numa certa empresa agrícola do interior do Mato Grosso afim de verificar a situação salarial dos funcionários dessa empresa. Para isso foram realizados alguns cálculos para análise dos dados.
Observe como foram distribuídos os salários dessa empresa.
a) Qual é a média salarial dessa empresa?
b) Qual é o salário mediano da empresa? E o salário modal?
c) O salário da maior parte dos funcionários está de acordo com a média? Por quê?
d) Há uma grande diferença entre os salários da empresa? Está abaixo ou acima da média?
e) Qual medida usar como base para melhor conclusão dos resultados? Por quê?
5-A professora Carla está realizando um projeto sobre o uso consciente da água. Para isso ela realizou uma pesquisa com os alunos da escola sobre o tempo que eles demoram no banho. Observe na tabela abaixo o tempo gasto pelos alunos do 8º ano.
Calcule a média, mediana e moda do tempo gasto pelos alunos do 8º ano.
6-Supondo que 5 minutos de banho é o suficiente para que não haja desperdício de água, podemos afirmar que o tempo gasto por esses alunos está de acordo com esse tempo? Porquê? O que significa dizer estar acima ou abaixo da média?
7-Numa turma de 3º ano do período noturno de uma escola os alunos possuem as seguintes idades:
16 17 15 16 16 17
16 17 18 16 19 18
17 18 19 17 16 18
A) Determine a média, a mediana e a moda desses dados. Que conclusões podemos tirar a partir desses valores?
B) Qual é a amplitude e o que isso representa?
SEQUÊNCIA DIDÁTICA – ESTATÍSTICA E PROBABILIDADE - Habilidade - EF08MA27
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Etapa 1 – Reúnam-se em duplas e preparem-se, agora é a vez de vocês pesquisarem. Nesta primeira etapa vocês precisarão definir o problema que irão investigar, então discutam e decidam um tema que seja de interessante e que possibilite a realização das outras etapas da pesquisa.
Etapa 2 – Esta etapa consiste no planejamento da pesquisa, é uma das etapas mais importantes, então não subestime esta fase. Anote tudo que será necessário fazer, todos os materiais que serão utilizados. É nesta fase que devem ser definidos as técnicas de coletas de dados, os procedimentos que serão seguidos para que se alcancem os resultados. Se a pesquisa for utilizar questionários estes já devem ser construídos para que se verifiquem possíveis alterações.
Etapa 3 – Após todo o planejamento, chegou a hora da coleta de dados. Nesta etapa tudo que foi planejado deve entrar em ação! Lembre-se de registrar tudo de maneira organizada para você não se perder depois.
Etapa 4 – Depois da coleta é preciso fazer a sistematização dos dados, isto é, organizá-los e decidir a melhor maneira de apresenta - los e verificar a necessidade de coletar mais dados ou fazer um recorte nos dados já coletados (em casos de grandes quantidades de dados). O leitor de sua pesquisa precisa saber o que você pesquisou, quais foram seus dados e seus objetivos, então tente escrever isso de
forma resumida para poder apresentar depois.
Etapa 5 – Agora chegou a esperada análise, nesta etapa vocês vão analisar seus dados de modo que possam tirar conclusões, então utilize gráficos variados, organize seus dados em tabelas, apresente a média moda e mediana destes dados.
Etapa 6 – Na sexta etapa vocês vão construir um texto com as conclusões obtidas na etapa anterior, então complemente o que você já escreveu na etapa 4, agora mostrando o que você encontrou na sua pesquisa.
Etapa 7 – Divulgando os resultados da pesquisa: toda pesquisa precisa ser divulgada, então use a criatividade, utilize os recursos digitais para divulgar sua pesquisa, faça cartazes com suas anotações, seus gráficos, mostre seus resultados, cole nos corredores da escola para que os outros possam ver o que você pesquisou.
Resolver agora os exercícios da Apostila volume 4 - 8ºAno
Página 121 - SITUAÇÃO DE APRENDIZAGEM 4 ATIVIDADE 1 – MÉDIA ARITMÉTICA SIMPLES - 1.1 e 1.2
Página 122 - ATIVIDADE 2 – MÉDIA ARITMÉTICA PONDERADA- 2.1 e 2.2
Página 123 - ATIVIDADE 3 – MODA E MEDIANA - 3.1 ; 3.2 e 3.3
Página 124 - ATIVIDADE 4 – CLASSE E INTERVALOS DE CLASSE 4.1 e 4.2
Página 125 -
Encontre o(s) número(s) que elevado(s) ao quadrado dê como resultado os quadrados perfeitos a seguir:
a) 49 = (7)² ou (−7)²
b) 81= (9)² ou (−9)²
c) 144= (12)² ou (−12)²
d) 625= (25)² ou (−25)²
Exercício 1






















Quais as respostas da 1-4° ?
ResponderExcluirOnde estão as respostas
ResponderExcluir