email
professorcarlosribeiro@yahoo.com
Habilidades EF07MA01
Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos.
Objetos de Conhecimento
Múltiplos e divisores de um número natural
Os múltiplos de um número inteiro são um conjunto cujos elementos são obtidos após a multiplicação desse número fixo por todos os números inteiros.
Exemplo:
Os múltiplos de um número inteiro são um conjunto cujos elementos são obtidos após a multiplicação desse número fixo por todos os números inteiros.
Os 15 primeiros múltiplos de 3.
Para determinar esse conjunto, basta multiplicar os 15 primeiros números inteiros por 3.
3 · 1 = 3 3 · 2 = 6 3 · 3 = 9 3 · 4 = 12 3 · 5 = 15 3 · 6 = 18
3 · 7 = 21 3 · 8 = 24 3 · 9 = 27 3· 10 = 30 3 · 11 = 33 3 · 12 = 36
3 · 13 = 39 3 · 14 = 42 3 · 15 = 45
Assim, os 15 primeiros múltiplos de 3 são:
M(3) = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45}
Exercício 1 -Encontre os 15 primeiros múltiplos dos números inteiros.
a)M(4)=
b)M(7)=
c)M(8)=
d)M(9)=
e)M(12)=
f)M(13)=
g)M(14)=
h)M(55)=
i)M(122)=
j)M(1512)=
Problemas que podemos resolver com múltiplos
Numa estação de ônibus há dois trajetos, o ônibus que faz trajeto passa a cada minutos e o do trajeto a cada . Considerando que os trajetos coincidam em determinado momento, em quantos minutos voltarão a se encontrar na estação?
Trajeto A Múltiplos de 30
M(30)={0,30,60,90,120,150,180,210,240,270,300,...}
Trajeto B Múltiplos de 50
M(50)={0,50,100,150,200,250,300,350,400,500...}
Note que o 1º momento é o de saída dos ônibus 0 e o próximo momento após a saída que os dois irão se encontrar será 150 minutos.
Resposta:Os ônibus irão se encontrar após 150 minutos ou como (1 hora =60 minutos) 60+60+30=150 (2horas e 30 minutos)
Observação
(Esse é um exemplo prático de exercício de M.M.C. (Menor Múltiplo Comum) MMC(30,50)=150
Resolva as seguintes situações Problemas:
01) Três navios fazem viagens entre dois portos. O primeiro a cada 6 dias, o segundo a cada 10 dias e o terceiro a cada 15 dias. Se esses navios partirem juntos, depois de quantos dias voltarão a sair juntos, novamente?
02) Em uma casa há três lâmpadas, a primeira acende a cada 27 horas, a segunda acende a cada 45 horas, a terceira acende a cada 60 horas . Após quantas horas as três lampâdas vão acender juntas?
03) Dois ciclistas saem juntos, no mesmo instante e no mesmo sentido, do mesmo ponto de partida de uma pista circular. O primeiro dá uma volta em 132 segundos e o outro em 120 segundos. Calcule os minutos que levarão para se encontrar novamente? (Observação 1 minuto=60 segundos)
04) Alguns cometas passam pela terra periodicamente. O cometa A visita a terra de 12 em 12 anos e o B, de 32 em 32 anos. Em 1910, os dois cometas passaram por aqui. Em que ano os dois cometas passarão juntos pelo planeta novamente?
Divisores
Divisores de um número natural são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero.
Exemplo:
Quais são os divisores do número 12?
12:1=12 RESTO 0 12:2=6 RESTO 0 12:3=4 RESTO 0 12:4=3 RESTO 0
12:5=2 RESTO 2 12:6=2 RESTO 0 12:7=1 RESTO 5 12:8=1 REST0 4
12:9=1 REST0 3 12:10=1 RESTO 2 12:11=1 RESTO 1 12:12= 1 RESTO 0
Analisando as divisões com resto zero temos:
Divisores de 12 = D(12)={1,2,3,4,6,12}
Exercicio 2- Encontre os divisores dos seguintes número naturais:
a) D(9)=
b)D(14)=
c)D(18)=
d)D(25)=
e)D(36)=
f)D(40)=
g)D(50)=
h)D(120)=
i)D(150)=
j)D(1000)=

Problemas que podemos resolver com divisores
Observe a seguinte situação: um carpinteiro tem dois pedaços de madeira de 30 e 60 centímetros cada um. Ele quer dividi-los em partes iguais com o maior tamanho possível sem que sobre nada. De quantos centímetros deve ser cada uma das partes?
D(30)={1,2,3,5,6,10,15,30}
D(60)={1,2,3,4,5,6,10,12,15,20,30,60)
Note que temos vários divisores comuns de 30 e 60, mas o que queremos é o maior deles no caso o 60.
Resposta: Cada uma das parte terá 30 centímetros ( ou seja 1 pedaço de 30 na 1ª madeira e 2 pedaços de 30 na 2ª madeira total 3 pedaços de 30cm).
Observação este é uma situação problema de MDC (Máximo Divisor Comum) ou Maior Divisor Comum MDC(30,60)=30
Exercício 3 -Resolver as seguintes situações problemas
Exercício 3 -Resolver as seguintes situações problemas
Um marceneiro quer aproveitar no máximo sua 3 tábuas e quer cortar elas sem perder madeira. Sabendo que uma tábua mede 240, outra 120 e 200 cm. Qual será o tamanho de cada tábua cortada?
Dona Estela vai cortar duas peças de tecidos de tamanho igual. Esse tamanho deve ser o maior possível. Uma peça tem 90 metros, a outra tem 78 metros. De que tamanho Dona Estela deve cortar cada pedaço de tecido?
Um marceneiro recebeu 40 toras, com 8 metros de comprimento cada uma, e 60 toras, com 6 metros de comprimento cada uma eles devem cortar todas estas toras em pedaços de mesmo tamanho e o maior possível. Qual será o tamanho de cada pedaço. E quantos pedaços serão obtidos?

observação (40x3=120 metros tora 1 e 60x6=360 metros tora 2 encontrar o maior divisor comum de 120 e 360)
Habilidades EF07MA07
Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas.
Objetos de Conhecimento
Fração e seus significados: como parte de inteiros, resultado da divisão, razão e operador
Fração
Fração é a forma de dividir alguma coisa através da razão de dois números inteiros. Dessa forma, nada mais é do que uma divisão onde o dividendo é numerador e o divisor é o denominador.
Quando dividimos uma pizza, por exemplo, estamos fracionando a pizza. Cada fatia representa uma parte da pizza, ou seja, uma fração. Geralmente ela é dividida em 8 pedaços, então cada pedaço de uma pizza representa 1⁄8 (um oitavo) de uma pizza.
Como representar uma fração?
Podemos representar uma fração através da escrita em números ou de forma visual, através de desenhos para melhor o entendimento. Vamos mostrar as duas formas.
Representação escrita de frações
Uma fração é representada, de forma escrita, por dois números inteiros, sendo um o numerador e o outro o denominador.
Exemplo:
Considere
Representação gráfica de frações
As frações também são representadas de forma gráfica. O aluno pode encontrar outra forma de representação gráfica, como, por exemplo, retângulos.
Nós vamos mostrar a forma mais usual de representação gráfica, que são os gráficos de pizza.
Vejas alguns exemplos:
Imagine uma pizza dividida em oito pedaços iguais, e caso exista quatro pessoas para comer esta pizza. Se todos comerem dois pedaços, assim cada pessoa comeu 2⁄8 (dois oitavos) de pizza.
Agora imagine que oito pessoas comeram um pedaço cada uma, dessa forma, cada pessoa comeu 1⁄8 (um oitavo) de pizza.
Como Encontrar uma Fração de um Número
Encontrar a fração de um número é o mesmo que multiplicar o número e a fração. Este método simples pode ser usado para qualquer tipo de número (porcentagem, fração, número misto, decimal), mas é mais fácil com números inteiros. Para resolver o problema, é preciso conhecer o básico das operações de multiplicação e divisão.
Exemplo;
1) Calcular 3/8 de 40
3.40/8 = 120/8 = 15
2) Calcular 3/5 de R$500,00
3.500/5 = 1500/5 = 300 Resposta R$300,00
3) A minha turma é formada por 42 alunos, dos quais 4/7 (quatro sétimos) são de meninas. Quantas meninas há na minha turma?
4/7 de 42 = 4.42/7 = 168/7 = 24
4) João comprou uma caixa com 24 laranjas. Seu pai pediu que separasse 7/12 ( sete doze avos) das maçãs para fazer suco e 3/8 (três oitavos) para fazer salada de frutas.
a) Quantas laranjas foram utilizadas para fazer suco?
7/12 de 24 = 7.24/12 = 168/12 = 14
b) Quantas laranjas foram utilizadas para a salada de frutas?
3/8 de 24 = 3.24/8 = 72/8 = 9
c) Quantas laranjas sobraram?
14+9 = 23 portanto 24 -23 = 1 sobrou 1 laranja
Exercício 4 - Fraçoes
1- Calcule:
a) 1/3 de 42. b) 1/8 de 92. c) 4/5 de 65. d) 9/7 de 63.
.2- Um grupo possui 120 pessoas, das quais 8/12 são mulheres e 4/12 são homens. Qual o número de
homens. Qual o número de mulheres?
3- De um curso com 104 alunos , 1/9 dos alunos são canhotos, quantos
estudantes são destros?
4- Quanto é 5/6 de R$3.500,00 ?
5- Mariana comprou uma caixa com 3500 bolinhas de ping pongue para revender. Mariana separou 3/5 dessas bolas para vender na loja A, 2/5 para a loja B . Quantas bolinhas de ping pongue cada loja recebeu?
6- Luciano pretender revestir o chão de sua casa, com ladrilhos com desenhos e sem desenhos. Seu pedreiro orientou que dos 125 ladrilhos 1/5 deles fossem com desenhos. Quantos ladrilhos serão com desenhos? Quantos serão sem desenhos?
7- Faça a representação de uma malha quadriculada com 5 quadradinhos na horizontal por 5 na vertical. Descubra quanto é 2/5 dos 25 quadradinhos e pinte essa quantidade na malha quadriculada.
8-Numa excursão de 60 pessoas, 5/6 são homens e o restante são mulheres. Quantos São as
mulheres?
9-Uma indústria automobilística produziu 1820 carros em agosto. Em setembro produziu apenas
3/5 dessa quantia. Quantos carros foram produzidos em setembro?
10-Se uma hora tem 60 minutos, quantos minutos são 3/4 da hora?
11-Uma prova de matemática tinha 40 questões. Paula acertou 5/8 delas. Quantas questões ela
acertou?
12- Num mês de 30 dias, diga quantos dias correspondem a 5/6 do mês?
Frações Equivalentes
s Frações Equivalentes são aquelas que aparentemente são diferentes, mas que possuem o mesmo resultado. Sendo assim, elas representam a mesma parte de um todo indicando a mesma quantidade.
Noções básicas
Antes de mais nada, devemos lembrar que nas frações o número localizado acima é chamado numerador e o que está abaixo é denominador:

2/4 e 4/8: se dividirmos o numerador e o denominador por 2 na fração 2/4, obtemos o valor 1/2.
Se dividirmos 4/8 por 2, obteremos o valor de 2/4. E se dividirmos novamente por 2, temos o valor 1/2.
Assim, as frações 1/2, 2/4 e 4/8 são frações equivalentes.
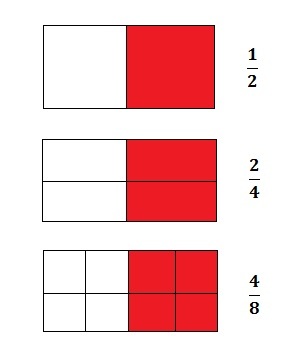 Representação de Frações Equivalentes
Representação de Frações Equivalentes
3/4 e 9/12: se dividirmos o numerador e o denominador da segunda por 3, obteremos o resultado da primeira: 3/4.
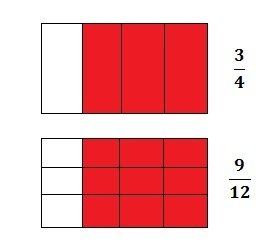 Representação de Frações Equivalentes
Representação de Frações Equivalentes
Note que as representações de cada uma são diferentes, mas o valor numérico resultante é igual.
Para encontrar frações equivalentes, basta multiplicar ou dividir o numerador e denominador pelo mesmo número. Esse número deve ser diferente de zero.
Frações equivalentes são frações que representam a mesma parte do todo.
Para encontrar frações equivalentes, devemos multiplicar o numerador e o denominador por um mesmo número natural, diferente de zero.
Exemplo: obter frações equivalentes à fração . 1/2
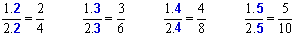
Portanto as frações
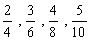 são algumas das frações equivalentes a 1/2.
são algumas das frações equivalentes a 1/2.A simplificação de frações é uma maneira de escrever a mesma fração, mas de forma que os numeradores e denominadores sejam escritos com números menores. Quando simplificamos uma fração, encontramos uma fração equivalente, porém na forma reduzida.
ara simplificarmos uma fração, devemos olhar para os números que estão no numerador e no denominador e encontrar algum número inteiro que divida de forma exata os dois números. Para melhor entender este processo, vejamos um exemplo:
.png)
Você poderia, a princípio, encontrar o número 2 que divide o numerador e querer simplificar esta fração por 2, mas lembre-se que o número escolhido deve dividir também o denominador. E, neste caso, o 2 não divide o número 9.
E o número 3, ele dividiria de maneira exata o numerador e o denominador?
6 dividido por 3 resulta em 2, e não sobra nenhum resto, ou seja, é uma divisão exata.
9 dividido por 3 resulta em 3 e não sobra nenhum resto, também uma divisão exata.
Com isso, encontramos um primeiro número que podemos utilizar na nossa simplificação.
E o número 3, ele dividiria de maneira exata o numerador e o denominador?
6 dividido por 3 resulta em 2, e não sobra nenhum resto, ou seja, é uma divisão exata.
9 dividido por 3 resulta em 3 e não sobra nenhum resto, também uma divisão exata.
Com isso, encontramos um primeiro número que podemos utilizar na nossa simplificação.
.png)
Note que a fração que obtemos é uma fração equivalente à nossa primeira fração, e o numerador e o denominador foram escritos com números reduzidos.
Você pode repetir esse processo até que não seja possível ter um número que divida o numerador e o denominador. No nosso primeiro exemplo não podemos simplificar novamente.
Vejamos outro exemplo:
Você pode repetir esse processo até que não seja possível ter um número que divida o numerador e o denominador. No nosso primeiro exemplo não podemos simplificar novamente.
Vejamos outro exemplo:
.png)
Veja que efetuamos a simplificação três vezes consecutivas, até obtermos uma fração totalmente reduzida, totalmente simplificada.
Observe que a cada simplificação feita os numeradores e denominadores foram reduzidos, isso se deve ao fato de estarmos obtendo frações equivalentes através da divisão e não da multiplicação.
Observe que a cada simplificação feita os numeradores e denominadores foram reduzidos, isso se deve ao fato de estarmos obtendo frações equivalentes através da divisão e não da multiplicação.
Exercício 5
1) Encontre 5 frações equivalente a:
A) 1/4=
B) 3/5=
C) 2/8=
D) 5/8=
E) 6/10=
2)Simplifique as frações:
A) 9/15=
B) 4/8=
C) 10/20=
D) 16/20=
E) 25/50=
Habilidades EF07MA02
Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.
Objetos de Conhecimento
Cálculo de porcentagens e de acréscimos e decréscimos simples
Porcentagem envolve diversas situações com que nos deparamos frequentemente em nosso cotidiano, por exemplo em indicadores econômicos, resultados de pesquisas ou promoções. Entendemos porcentagem como sendo a razão entre um número qualquer e 100, sendo representada pelo símbolo %. Utilizamos a ideia de porcentagem para representar partes de algo inteiro.
Sabemos que a porcentagem é uma razão, logo, pode ser representada por uma fração, que, por sua vez, pode ser escrita na forma decimal. De modo geral, se temos um número acompanhado pelo símbolo %, basta dividi-lo por 100, ou seja:
Veja os exemplos seguintes que mostram as diferentes representações de porcentagens. Lembre-se, para “transformar” a porcentagem em fração, basta dividir o número que acompanha o símbolo % por 100 e simplificar a fração; para “transformar” a fração em forma decimal, basta realizar a divisão.
Exemplos
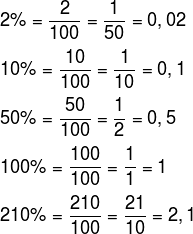
Perceba que quando escrevemos a porcentagem 100% é o mesmo que considerar um inteiro, ou seja, quando consideramos 100% de algo, estamos levando em conta o total daquilo. No caso de 210%, estamos considerando mais que um inteiro, isto é, consideramos 2,1 vezes o total.
Para fazer o caminho de volta, ou seja, dado uma fração ou um número decimal para ser escrito na forma percentual, basta multiplicar o número em questão por 100. Veja:
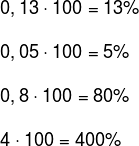
Como calcular a porcentagem?
Para realizar o cálculo da porcentagem de um valor, basta multiplicar esse valor pela porcentagem em sua forma decimal ou fracionária.
Exemplos
- Calcule 50% de 600.
50% de 600
50/100.600
50.600=30000/100=300
Logo, 50% de 600 = 300. Veja que 50% representam a metade do total que é 600.
1) Calcule as porcentagens correspondentes:
a) 2% de 700 laranjas
b) 40% de 48 metros
c) 38% de 200 Kilos
e) 45% de 1000 chocolates
Habilidades EF07MA06
Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos.
Objetos de Conhecimento Fração e seus significados: como parte de inteiros, resultado da divisão, razão e operador.
Exercício 7
Observação: ((Lucro) pego resultado e soma com a porcentagem obtida))
((Prejuízo)) pego o resultado e subtrai com a porcentagem obtida)
1) Uma loja de calçados vendeu 1.800 calçados no mês passado, neste mês vendeu 10% a mais. Quantos calcados foram vendidos esse mês?
10% de 1800 = 10/100.1800= 0,1.1800 =180
Portanto 1800+180=1980
Alternativa B correta
A) ( ) 1900
Alternativa B correta
A) ( ) 1900
B) ( x ) 1980
C) ( ) 2000
2) Uma empresa teve em seu caixa RṨ2.500,00 reais e o seu lucro é de 15% do valor do caixa. Qual é o seu lucro?
A) ( ) 300,00
B) ( ) 350,00
C) ( ) 375,00
3) O atacadista teve em seu lucro em R$980,00 e vai investir 30% do seu lucro em mercadorias. Qual é o valor que vai ser investido?
A) ( ) 250,00
B) ( ) 294,00
C) ( ) 300,00
4) O valor do caminhão no mercado é de R$290.000,00 e o supermercado comprou 50% mais barato. Qual foi valor do caminhão?
A) ( ) 145.000,00
B) ( ) 150.000,00
C) ( ) 200,000,00
5) A mercearia tem R$500,00 em caixa e 40% é para as despesas. Qual é o valor para as despesas?
A) ( ) 100,00
B) ( ) 150,00
C) ( ) 200,00
6) Sabe-se que 38% de uma distância x corresponde a 600 m. Qual a distância x?
7) Uma escola tem 25 professores, dos quais 24% ensinam Matemática. Quantos professores ensinam Matemática nessa escola?
8) Na compra de um aparelho obtive desconto de 15% por ter feito o pagamento à vista. Se paguei R$ 120,00 reais pelo aparelho, qual era seu o preço original?
9) Na compra de uma mala de viagem, três lojas oferecem os descontos a seguir. En que loja será mais vantajoso financeiramente comprar a mala de viagem. Justifique sua resposta.
Loja A Preço R$82,00 com 5% de desconto à vista
Loja B Preço R$90,00 com 8% de desconto à vista
Loja C Preço R$85,00 com 10 % de desconto à vista.
10) Leonardo pegou um empréstimo de 1000 reais e vai pagar em 10 prestações de 100 reais com juros de 2% ao mês. Qual o total pago por Leonardo ao quitar sua dívida?
Habilidades EF07MA13
Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita.
Objetos de Conhecimento
Linguagem algébrica: variável e incógnita
Problemas com números desconhecidos
A matemática pode ser usada diariamente para resolver diversos problemas que giram em torno de números desconhecidos, comumente representados por letras.
Por exemplo:
Qual é o número que somado com 12 tem como resultado 25?
Para resolver esse problema, devemos escolher os números e realizar os cálculos.
Resolução
X – número desconhecido
x + 12 (número desconhecido somado a 12)
x+12=25 (equação do problema)
Para descobrir o valor desconhecido basta fazer a operação inversa da adição que é a subtração. Confira:
x+12 = 25
x= 25-12
x=13
Logo o valor desconhecido é o 13.
Exercício 8
Leia as expressões abaixo, transponha para a linguagem matemática e encontre o valor desconhecido.
Exercício resolvido
A) Que numero preciso somar a 46 pra obter 97?
numero= x
somado a 46 = x+46
Expressão x+46=97
x=97-46
x= 51
Resposta: O valor será desconhecido será o 51
B) Que número devo somar a 54 para obter 99?
C) Que número devo somar a 345 para obter 549?
D)Que número devo subtrair de 565 para obter 760?
E)Que numero devo subtrair de 1056 para obter 456?
F)Que número devo multiplicar por 3 para obter 27?
G)Que número de multiplicar por 9 para obter 54?
H)Que número devo dividir por 5 para obter 9?
i)Que número devo dividir por 7 para obter 9?
Observação: Operação inversa soma é a subtração
Operação inversa subtração é a soma
Operação inversa da multiplicação é a divisão
Operação inversa da divisão é a multiplicação
Podemos utilizar outras letras para representar essa expressões algébricas
Exemplos:
Um número somado a 25 é igual a 32 A+25=32
O dobro de um número somado a 40 é igual a 60 2.A +40 = 60
O triplo de um número subtraído de 10 é igual a 5 3.N -10 = 5
O quadruplo de um número somado a 20 é igual a 60 4.p+20= 60
A metade de um número somado a 5 é igual a 25 T/2 +5 = 25
A terça parte de um número subtraído de 5 é igual a 0 X/3 - 5 = 0
Como resolver essa expressões? Basta usar o mesmo conceito da operação inversa.
A+25 =32 A=32-25 A=7
2.A + 40 = 60 2.A= 60-40 2.A=20 A=20/2 A=10
3.N-10=5 3.N=5+10 3.N=15 N=15/3 N=5
4.P+20 =60 4.P=60-20 4.P=40 P=40/4 P=10
T/2+5=25 T/2=25-5 T/2= 20 T=20.2 T=40
x/3-5=0 x/3=0+5 x/3=5 x=5.3 x=15
EXERCÍCIO 9
Leia as expressões abaixo, transponha para a linguagem matemática e descubra o valor desconhecido.
1-Exercício resolvido:
O dobro de um número somado a 10 é igual a 90
dobro do número = 2.N
somado a 10 = +10
Expressão matemática 2.N+10=90
2.N+10=90 2.N=90-10 2.N=80 N=80/2 N=40
2- O dobro de um numero somado a 50 é igual a 100.
3- O dobro de um número somado a 350 é igual a 400.
4- O dobro de um número subtraído de 100 é igual a 50.
5- O triplo de um número somado a 45 é igual a 90.
6- O triplo de um número subtraído de 15 igual a 15
7- O quadruplo de um número somado a 10 é igual a 90.
8- A metade de um número somado a 10 é igual a 50.
9- A metade de um número somado a 25 igual a 50.
10- A terça parte de um número somado a 9 é igual a 27
Situações problema envolvendo expressões algébricas
1- Uma determinada empresa de aluguel de bicicletas cobra um valor fixo de R$3,00 para o aluguel das bicicletas e R$ 1,50 por Kilômetro rodado com a bicicleta. Se uma uma pessoa rodar 18 Kilômetros com a bicicleta, qual ao valor final a ser pago?
Transpondo para a linguagem matemática:
Valor Fixo (VF)
Kilõmetro (Km)
Valor Pago (VP)
Montando a expressão;
Valor Pago = Valor Fixo + 1,50 . Kilômetro rodado
(VP) = VF + 1,50 . Km
(VP) = 3,00 + 1,50.18
(VP) = 3,00 + 27,00
(VP) = 30,00
2- No Brasil, o número de sapato está relacionado com o tamnho do pé, em centímetros, e é dado pela seguinte fórmula:
N= 5.P+28/4
Onde:
N é o número do sapato
P é o tamanho do pé em centímetros
Exemplos:
A) Eu calço sapato 40 e meu pé mede 26 cm.Então
N=5.P+28/4
N=5.26+28/4N=130+28/4
N=158/4
N=39,5
Arrendondando, encontramos 40 que é exatamente o número que calço.
Arrendondando, encontramos 40 que é exatamente o número que calço.
B) Minha esposa calça sapatos número 36. Seu pé mede 23cm. Vejamos:
N=5.P+28/4
N=5.23+28/4N=115+28/4
N=143/4
N=35,75
Arrendondando, encontramos 36, que é exatamente o número do calçado da minha esposa.
C) Uma mãe consultou o farmacêutico sobre o número de gotas de um remédio recomendado para crianças. Antes de responder ele leu as seguintes instruções na bula:
IDADE DA CRIANÇA NÚMERO DE GOTAS
1 ano 2.P
2 anos 2.P-5
3 anos 2.P-8
4 anos 2.P-10
A mãe informou que a criança tinha 2 anos e 11 Kg.Quantas gotas ela deveria usar?
2 anos uso a expressão 2.P-5
P= peso em kg = 11kg
2.P-5= número de gotas
2.11-5 = número de gotas
22-5= número de gotas
17= número de gotas
Resposta: A criança deve tomar 17 gotas do remédio.
Exercício 10
Transponha para a linguagem matemática as seguintes situações problemas e encontre o valor desconhecido.
A) Uma empresa de transporte de pessoas de carros por aplicativo, cobra um valor fixo de R$2,50 por viagem mais R$0,90 por kilômetro rodado. Qual o valor final de uma corrida em que ele percorreu 24 Kilômetros?
B)Uma determinada empresa calcula o valor de cada unidade de mascara de proteção com a seguinte fórmula;
Valor Final= Valor Fixo + 0,45 . Unidade Produzida
(VF) = 1,50 + 0,45 . UP
B1) Qual o valor final de um pedido de 1500 unidades?
B2) Qual o valor final de um pedido de 70000 unidades?
B3)Qual o valor final de um pedido de 800000 unidades?
C) Usando a fórmula do exemplo 2 .Qual o número do calçado que uma pessoa deve comprar se o seu pé medir 22 cm?
D)Usando a fórmula do exemplo C quantas gotas uma criança de 4 anos deve tomar desse mesmo remédio do exemplo C?
Observação:
O valor fixo geralmente esta associado aos custos fixos ( no exemplo do carro de aluguel (manutenção mecânica do carro,IPVA), no caso das mascaras ( aluguel do imóvel, água, luz, manutenção das máquinas, salário do funcionário,etc)
O valor fixo geralmente esta associado aos custos fixos ( no exemplo do carro de aluguel (manutenção mecânica do carro,IPVA), no caso das mascaras ( aluguel do imóvel, água, luz, manutenção das máquinas, salário do funcionário,etc)
Habilidades EF07MA22
Construir circunferências, utilizando compasso, reconhecê-las como lugar geométrico e utilizá-las para fazer composições artísticas e resolver problemas que envolvam objetos equidistantes.
Objetos de Conhecimento
A circunferência como lugar geométrico
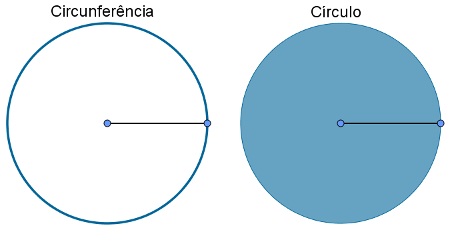
Os elementos do círculo e da circunferência são raio, diâmetro, corda, arco da circunferência, setor circular e coroa circular, entre outros.
Para um dado ponto C, chamado centro, uma circunferência é o conjunto de todos os pontos que possuem uma distância fixa até C. Essa distância geralmente é representada pela letra r. Os círculos, por sua vez, são compostos por todos os pontos de uma circunferência e por seus pontos interiores. A imagem a seguir ilustra uma circunferência e um círculo.
Destacamos a seguir os elementos dessas duas figuras, que possuem grande importância para a Geometria:
1 – Raio
O raio é a distância entre um ponto de uma circunferência e seu centro. O raio do círculo é a distância entre a borda do círculo e seu centro.
Dizemos que um ponto é interior a uma circunferência quando a sua distância até o centro é menor que o raio; o ponto é externo quando a distância entre o centro e ele é maior que o raio; e, por fim, dizemos que um ponto pertence a uma circunferência quando sua distância até o centro é igual ao raio.
O raio da circunferência (e/ou do círculo) é indispensável em cálculos, como comprimento, área etc.
O comprimento da circunferência é dado pela seguinte fórmula:
C = 2πr
E a área do círculo é obtida pela fórmula a seguir:
A = πr2
Em ambos os casos, r é o raio da circunferência (ou do círculo) e π é uma constante de aproximadamente 3,1415.
2 – Cordas
Em uma circunferência, a corda é qualquer segmento de reta que liga dois de seus pontos. Atenção: o centro não é ponto da circunferência!
Dessa maneira, as cordas, em um círculo, podem ser compreendidas como segmentos de reta que ligam dois pontos distintos de sua borda.

3 – Diâmetro
O diâmetro é uma corda da circunferência que contém o centro. Dessa maneira, o diâmetro é a maior corda possível em uma circunferência e sua medida é igual a duas vezes o raio.
Diametro = 2·raio
O resultado da divisão entre o comprimento de uma circunferência e o seu diâmetro sempre será igual a uma constante, representada pela letra grega π, que é aproximadamente 3,14. Isso independe do tamanho da circunferência, pois seu comprimento e seu diâmetro são proporcionais e a razão de proporcionalidade é igual a π.
uma circunferência. As duas partes formadas que vão de A até B são chamadas de arcos da circunferência, como demonstrado na figura a seguir:
Em outras palavras, o arco é uma parte de uma circunferência limitada por dois pontos.

O compasso é um objeto usado para desenhar círculos e circunferências
Exercício 11
Com o auxilio de um compasso construa uma circunferência de raio 5 centímetros e identifique nessa circunferência o seu Raio e seu diâmetro.
B) Com auxilio da fórmula comprimento = 2.𝞟.r calcule o comprimento dessa circunferência que você desenhou.
C) Construa duas circunferências concêntricas, com a mesma origem uma com raio 3,5 cm e outra com raio 4,5 cm.
Habilidades EF07MA24
Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é 180°.
Objetos de ConhecimentoTriângulos: construção, condição de existência e soma das medidas dos ângulos internos
Um triângulo é uma figura geométrica que possui três lados, três ângulos e três vértices. Os triângulos possuem diversas propriedades, uma delas diz respeito aos seus ângulos internos: independentemente das dimensões do triângulo, do seu formato, do comprimento de seus lados ou da medida de seus ângulos internos, a soma desses ângulos internos sempre será igual a 180°.
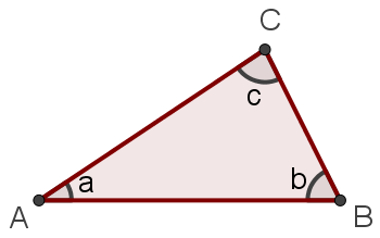
Em outras palavras, se ABC é um triângulo, e a, b e c são seus ângulos internos, como podemos exemplificar com a imagem a seguir:
Então, podemos escrever corretamente a soma:
a + b + c = 180°
Geralmente, essa igualdade não é usada para descobrir que a soma dos ângulos internos de um triângulo é igual a 180°, mas sim para determinar a medida de um dos ângulos internos de um triângulo, quando as medidas dos outros dois são conhecidas.
Exemplo: Qual a medida do terceiro ângulo interno de um triângulo que possui dois ângulos internos iguais a 30° e a 90°?
Solução:
30° + 90° + x = 180°
x = 180° – 30° – 90°
x = 60°
x = 180° – 30° – 90°
x = 60°
O terceiro ângulo mede 60°.
Demonstração
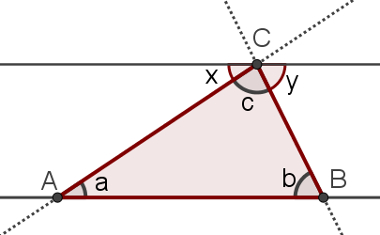
Considere o triângulo ABC, com ângulos a, b e c, como o da figura a seguir:
Construa sobre o ponto C uma reta paralela ao lado AB desse triângulo.
Reta paralela ao lado AB no triângulo ABC
Observe que os lados AC e BC podem ser encarados como retas transversais, que cortam as duas retas paralelas. Os ângulos x e y formados nessa construção são, respectivamente, alternos internos com os ângulos a e b. Assim, x = a e y = b.
Agora, note que a soma x + c + y = 180°, pois os três ângulos são adjacentes e seus limites são a reta paralela ao lado AB. Assim, substituindo os valores de x e y, teremos:
a + b + c = 180°
Exemplos:
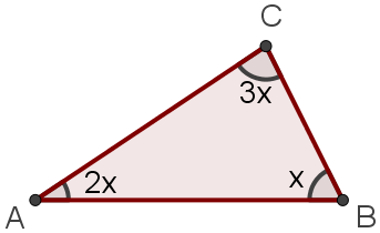
1º Exemplo – Determine a medida de cada um dos três ângulos internos do triângulo a seguir.
Solução:
Sabendo que a soma dos ângulos internos de um triângulo é igual a 180°, basta fazer:
x + 2x + 3x = 180°
6x = 180°
x = 180°
6
x = 30°
6x = 180°
x = 180°
6
x = 30°
Como os ângulos internos são múltiplos de x, cada um deles mede:
x = 30°,
2x = 60° e
3x = 90°
2x = 60° e
3x = 90°
2º Exemplo – Um triângulo tem um de seus ângulos internos com a medida exatamente igual ao triplo das medidas dos outros dois, que são congruentes. Quanto mede cada um dos ângulos internos desse triângulo?
Solução:
Para resolver esse problema, considere que os dois ângulos congruentes medem x e o outro ângulo mede 3x. Como a soma dos ângulos internos é igual a 180°, teremos:
x + x + 3x = 180°
5x = 180°
x = 180°
5
x = 36°.
5x = 180°
x = 180°
5
x = 36°.
Como x é a medida dos dois ângulos congruentes, já sabemos que eles medem 36°. O terceiro ângulo é o triplo disso, portanto, mede:
3x = 3·36 = 108°
Exercício 12
A) – Qual é a medida do ângulo α na figura a seguir?
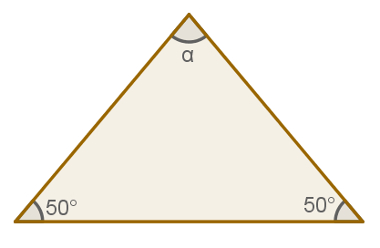
B) – Calcule o valor de x no triângulo a seguir.
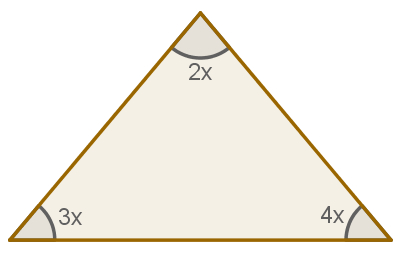
Habilidades EF07MA29
Resolver e elaborar problemas que envolvam medidas de grandezas inseridos em contextos oriundos de situações cotidianas ou de outras áreas do conhecimento, reconhecendo que toda medida empírica é aproximada.
Objetos de Conhecimento
Problemas envolvendo medições
Exercício 13
A) Marcos vai a pé para a escola. Seu trajeto de casa para a escola tem aproximadamente 550 metros. Sabendo que o passo de Carlos mede 35 centímetros, calcule quantos passa marcos dá para ir da casa até a escola?
B) Diana percorre diariamente 10 Quilômetros, mas na segunda-feira só conseguiu correr 3/5 dessa distância. Quantos metros ele correu na segunda feira?
C) Um depósito de materiais de construção ensaca areia em embalagem de 2 tamanhos; O 1º saco de 15 quilos custa 2 reais e o de 40 quilos custa 5 reais. Para fazer o acabamento do meu banheiro, vou precisar de 150 quilos. Quantos sacos de areia, de cada tamanho, devo comprar pagando o menos valor possível?
D) Em uma sala quadrada foram gastos 24,80 m de rodapé de madeira. A sala tem apenas uma porta de 1,20 m de largura. Considerando que não é necessário colocar rodapé no local da porta, calcule a medida de cada lado desta sala.
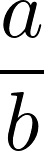







.jpg)

onde acesso o dever de casa por aqui?
ResponderExcluir