Números -7º ano
Habilidade - (EF07MA12) - Resolver e elaborar
situações problema que envolvam as operações com números racionais.
SITUAÇÃO DE APRENDIZAGEM 1
ATIVIDADE 1 – OS NÚMEROS E SUAS DIFERENTES
REPRESENTAÇÕES
03/08 - 7º ano EF - Matemática - Operações com racionais: Parte I
04/08 - 7º ano EF - Matemática - Operações com racionais: Parte II
05/08 - 7º ano EF - Matemática - Operações com racionais: Parte III
10/08 - 7º ano EF - Matemática - Operações com racionais: IV
Representação diferentes dos números
Exemplos
Represente os números nas ordem de unidades
simples.
A) 1,4mi = 1 mil e 400 = 1.400
B) 7,3 mi = 7 mil e 300 = 7.300
C) 5,4milhões = 5 milhões e 400 mil
= 5.400.000
D) 7,34 milhões = 7 milhões e 340 mil = 7.340.000
E) 2,4 bilhões = 2 bilhões e 400 milhões = 2.400.000.000
F) 5,67 bilhões = 5 bilhões e 670 milhões = 5.670.000.000
F) O INSS sofre com a redução pessoal. Só no ano passado, mais de 5,7 mil servidores do órgão se
aposentaram. Além disso, de acordo com o jornal "O Estado de S.
Paulo", cerca de 20% do quadro de funcionários ativos do INSS está em
licença-saúde. A Secretaria de Previdência admitiu que o atraso nas análises se
deve, entre outros fatores, a uma redução da força de trabalho do INSS.... -
Veja mais em https://economia.uol.com.br/noticias/redacao/2020/01/18/inss-pedidos-atrasados-aposentadoria-beneficios-medidas-governo.htm?
5,7
mil = 5 mil
e 700 = 5.700
G) De acordo com uma nota técnica da Secretaria de
Previdência, havia quase 1,9 milhão de pedidos acumulados em 1ª de janeiro de 2019... - Veja
mais em https://economia.uol.com.br/noticias/redacao/2020/01/18/inss-pedidos-atrasados-aposentadoria-beneficios-medidas-governo.htm?
1,9
milhões = 1
milhão e 900 mil = 1.900.000
Exercício 1
A)
3,7
mi
B)
6,8mi
C)
5,9mi
D)
4,5
milhões
E)
7,89
milhões
F)
5,6
bilhões
G)
4,93
bilhões
H)
INSS tem 1,3 mil de pedidos atrasados; como aconteceu e o que será feito?... -
Veja mais em https://economia.uol.com.br/noticias/redacao/2020/01/18/inss-pedidos-atrasados-aposentadoria-beneficios-medidas-governo.htm?
I)
Parte dos militares deve ser direcionada ao atendimento nas
agências, para substituir os servidores do próprio INSS, que serão remanejados
para a análise dos benefícios. O custo estimado pelo governo é de R$ 14,5 milhões ao mês durante nove
meses. Ao todo, um gasto de R$ 130,5 milhões... - Veja mais em https://economia.uol.com.br/noticias/redacao/2020/01/18/inss-pedidos-atrasados-aposentadoria-beneficios-medidas-governo.html
Fração na forma Decimal
½= 1:2 = 0,5
¾= 3:4 = 0,75
2/5 = 2:5 = 0,4
J)
Resolver exercício pagina 63
apostila 7º ano volume 3
Exercício 1.1
e exercício 1.2
Como encontrar frações equivalentes?
Para encontrar uma fração equivalente, basta multiplicar os numeradores
e denominadores por algum número natural que seja diferente de zero. Mas,
lembre-se, tudo que for feito no numerador deve ser igualmente feito no
denominador. Veja alguns exemplos:
Frações equivalentes a 1/5
1 = 2 = 4 = 8 = 16 (todas
as frações foram multiplicadas por 2)
5 10 20
40 80
1 = 3 = 9 = 27 = 81 (todas
as frações foram multiplicadas por 3)
5 15 45
135 405
1 = 5 = 25 = 125 = 625
5
25 125
625 3.125
(todas frações multiplicadas por 5)
Exercício2: EQUIVALÊNCIA
Resolver exercício apostila volume 3 página 63
Exercício 2.1 e 2.2
Exercício 2.3
Exercício 2.4 ; 2.5 ; 2.6 ; 2.7 e 2.8
Exercício 3
Resolver exercício apostila volume 3 página 65
Exercício 3.1 ; 3.2 ; 3.3 e 3.5
A multiplicação de frações é realizada multiplicando o
numerador da primeira fração com o numerador da segunda fração e
em seguida multiplicando o denominador da primeira com o denominador da
segunda. A operação continua sucessivamente em casos em que a multiplicação envolvem
mais de duas frações.
Exercício 4
Resolver exercício apostila volume 3 página 66
3.6 e 3.7
Divisão de Frações
Divisão de
uma fração por outra fração
Dividir fração por fração pode parecer um
pouco complicado, pois a forma escrita fica um pouco esquisita. Mas é bem
simples. Veja!
Dividir 3⁄5 por 7⁄3
Copiamos a primeira e multiplicamos pelo
inverso da segunda. Multiplicando os números de cima e de baixo.
Exercício 5
Resolver as divisões de
frações por frações
Álgebra – 7º Ano
Habilidade - (EF07MA16) - Reconhecer se duas
expressões algébricas obtidas para
descrever a regularidade de uma mesma sequência numérica são ou não
equivalentes.
11/08 - 7º ano EF - Matemática - Expressões algébricas equivalentes: Parte I
12/08 - 7º ano EF - Matemática - Expressões algébricas equivalentes: Parte II
Utilizando a Propriedade Distributiva na Resolução de Equações
Princípio da Propriedade Distributiva da Multiplicação
a * (b + c) → ab + ac
2 * (x – 1 ) → 2x – 2
4 * (y – 2) → 4y – 8
6 * (x + 4) → 6x + 24
Exemplo 1
8 (x + 2) = 4 (x + 6) → aplicar a propriedade distributiva
8x + 16 = 4x + 24
8x – 4x = 24 – 16
4x = 8
x = 8 / 4
x = 2
Exemplo 2
8 (x + 3) = 40 → aplicar a propriedade distributiva
8x + 24 = 40
8x = 40 – 24
8x = 16
x = 16 / 8
x = 2
8 (x + 2) = 4 (x + 6) → aplicar a propriedade distributiva
8x + 16 = 4x + 24
8x – 4x = 24 – 16
4x = 8
x = 8 / 4
x = 2
8 (x + 3) = 40 → aplicar a propriedade distributiva
8x + 24 = 40
8x = 40 – 24
8x = 16
x = 16 / 8
x = 2
02/09 - 7º ano EF - Matemática - Proporcionalidade: Parte 3
14/09/2020 - 7º ano EF - Matemática - Reta e ângulo: Parte II
15/09/2020 - 7º ano EF - Matemática - Reta e Ângulos: Parte III
Retas paralelas, concorrentes e perpendiculares
As retas paralelas não se cruzam. Na figura abaixo representamos as retas paralelas r e s.
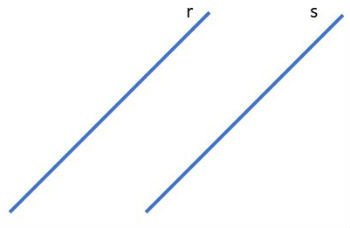
Diferente das retas paralelas, as retas concorrentes se cruzam em um único ponto.
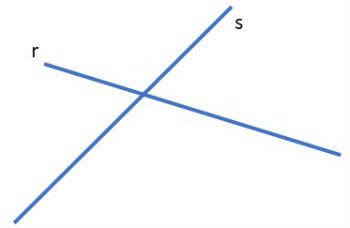
Se duas retas se cruzam em um único ponto e o ângulo formado entre elas no cruzamento for igual a 90º as retas são chamadas de perpendiculares.
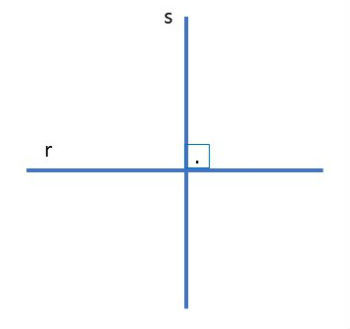
Retas paralelas cortadas por uma transversal
Uma reta é transversal a uma outra se possuem apenas um ponto em comum.
Duas retas paralelas r e s, se forem cortadas por uma reta t, transversal a ambas, formará ângulos como representados na imagem abaixo.
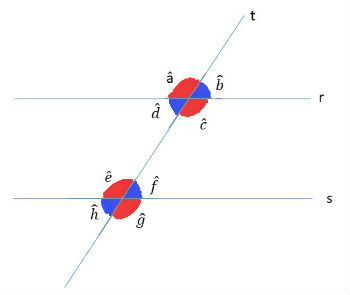
Por exemplo, os ângulos a e c apresentam mesma medida e a soma dos ângulos f e g é igual a 180º.
- Correspondentes
- Alternos
- Colaterais
Ângulos correspondentes
Dois ângulos que ocupam a mesma posição nas retas retas paralelas são chamados de correspondentes. Eles apresentam a mesma medida (ângulos congruentes).
Os pares de ângulos com a mesma cor representados abaixo são correspondentes.
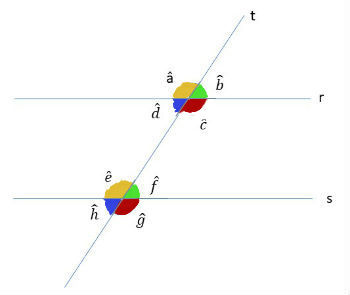
Na figura, os ângulos correspondentes são:
- a e e
- b e f
- c e g
- d e h
Ângulos Alternos
Os pares de ângulos que estão em lados opostos da reta transversal são chamados de alternos. Esses ângulos também são congruentes.
Os ângulos alternos podem ser internos, quando estão entre as retas paralelas e externos, quando estão fora das retas paralelas.
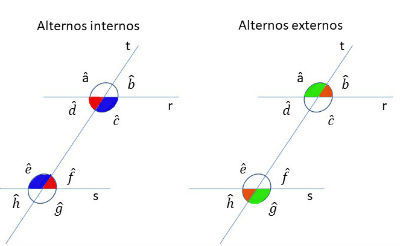
Na figura, os ângulos alternos internos são:
- c e e
- d e f
Os ângulos alternos externos são:
- a e g
- b e h
Ângulos colaterais
São os pares de ângulos que estão do mesmo lado da reta transversal. Os ângulos colaterais são suplementares (somam 180º).Também podem ser internos ou externos.
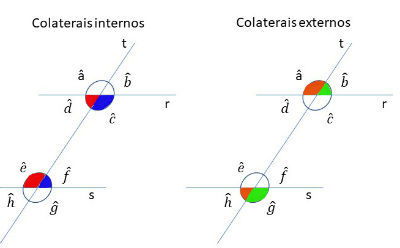
Na figura, os ângulos colaterais internos são:
- d e e
- c e f
Os ângulos colaterais externos são:
- a e h
- b e g
Exercícios
1) Observando os ângulos entre as retas paralelas e a reta transversal, determine os ângulos indicados na figura:
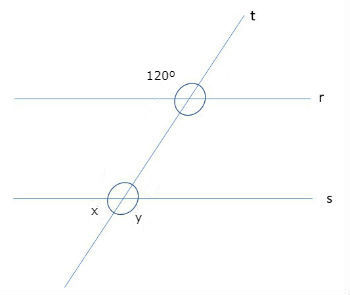
O ângulo dado e o ângulo x são colaterais externos, portanto a soma dos ângulos é igual a 180º. Desta forma, a medida do ângulo x é 60º.
Já o angulo dado e o ângulo y são alternos externos, portanto, são congruentes. Assim, a medida do ângulo y é 120º.






Nenhum comentário:
Postar um comentário