Atividade 1 - 4º Bimestre
Professor Carlos Ribeiro Cardoso - 7ºC
SEQUÊNCIA DIDÁTICA –
ÁLGEBRA –
Habilidade - EF07MA18
(EF07MA18) Resolver e
elaborar problemas que possam ser representados por equações polinomiais
de 1º grau, redutíveis à forma ax + b = c, fazendo uso das propriedades
da igualdade.
Quadro 1 – seria 3x+5=20
Quadro
2 – Se compro 3 laranjas + 5 reais em uvas e tudo
custa 20 reais por quanto saiu cada laranja
Quadro
3 – Se chamo cada laranja de X e assumo o valor das uvas que é R$5,00 totalizando
uma compra de 20 reais como representar essa igualdade?
Com base no Quadro acima, responda as questões a seguir:
1-Pai
Gonçalo inicia o desafio aos irmãos perguntando a Vitória a seguinte
questão: se fui ao mercado comprar 5 pacotes de bolachas do tipo doce e 7
reais em refrigerantes, mas a compra deu um valor total de 15 reais, por
quanto saiu cada pacote de bolacha doce? Escreva a expressão na forma de
uma equação de grau 1 e identifique o valor procurado.
__________________________________________________________
__________________________________________________________
2-Em seguida, pai Gonçalo
informou ao Vinicius de que um grupo de amigos realizaram a compra de 25
reais em doces e dividiram a conta entre eles, sabe se que cada um paga 4 reais
e ainda faltava 5 reais para pagar a conta. Qual a equação que representa
esta situação? E qual a quantidade de crianças que realizaram a
compra?
__________________________________________________________
__________________________________________________________
3-Pai
Gonçalo ainda questionou aos irmãos se ao comprarem 8 pastéis de queijo
para o lanche de hoje, e ainda pagar outros 8 reais e refrigerantes
para
acompanhar, por quanto deve
ser o preço máximo de cada pastel para que 50 reais seja necessário para
pagar a conta?
________________________________________________________________
________________________________________________________________
4-Satisfeito
com as respostas dos irmãos, pai Gonçalo resolveu apresentar uma lista de
expressões e pediu para que Vinícius identificasse qual delas representa
a expressão da seguinte situação: O caminhão de entrega de tomates para o
mercado de cobra 500 reais de frete para percorrer 150 km de distância, e
ainda cobram 100 reais para o pagamento de pedágio. Qual expressão
utilizar para identificar por quanto sairá cada km rodado pelo entregador
se somado todos os custos?
A) ( ) 150x = 600;
B) ( ) 500x – 100 = 150;
C) ( ) 100 + 150x = 500;
D) ( ) 500 – 150x = 100
5-Sabendo
que Vitória gosta muito de andar de cavalinho no circo, e que ao guardar
o dinheiro de sua mesada, ela só conseguiu o montante de 34 reais, e que o
valor do ingresso para brincar no cavalinho é 3 reais, e ainda, que ela
precisa guardar 7 reais para um lanche após a brincadeira, perguntou a
menina, quantas vezes ela poderia brincar no cavalinho e ainda guardar 7
reais para o lanchinho?
A) ( ) 10;
B) ( ) 7;
C) ( ) 8;
D) ( ) 9.
6-Pai
Gonçalo gostou tanto dos desafios que resolveu comprar 3 pastéis e pagou
8 reais em refrigerantes. Sabendo que o total pago foi de R$ 23,00, qual o
valor pago por cada pastel?
__________________________________________________________
__________________________________________________________
7-Por
fim, já satisfeito com os desafios enfrentado e vencidos pelos irmãos
Vitória e Vinícius, pai Gonçalo resolveu pedir para que os irmãos
elaborassem um probleminha que pudesse depois ser representado na forma
de uma expressão como a equação de grau 1º, como as que já estavam
estudando. Se fosse você, como responderia à questão?
__________________________________________________________
__________________________________________________________
8- Uma pesquisa de preços dos produtos foi realizada em supermercados
durante uma semana do mês de novembro.
Batata – R$2,50 o kilo
Feijão – R$3,20 o kilo
Arroz – R$8,50 o Kilo
A) Escreva
uma expressão algébrica para representar o gasto para a quantidade de qualquer
produto.
Resolução:
Chamando de X a quantidade de produtos
Batata – Preço =
2,50 . X
Feijão - Preço = 3,20 . X
Arroz - Preço = 8,50 . X
B) Utilizando as
expressões algébricas quanto você pagaria em 5 kilos de cada produto.
Resolução:
Basta
trocar o X por 5
Batata
– Preço =2,50 . X
Preço = 2,50 . 5
Preço = R$12,50
Feijão – Preço =
3,20 . X
Preço
= 3,20 . 5
Preço
= 16,00
Arroz – Preço = 8,50
. X
Preço
= 8,50 . 5
Preço = 42,50
C) Comprando
3 kilos de arroz e pagando com uma nota de R$50,00 . Escreva uma expressão
algébrica para representar essa situação e depois descubra o valor do troco
recebido.
Resolução:
Preço do arroz =( 8,50.X)
Expressão:
Troco = 50 – (8,50.X)
Troco = 50 - (8,50 . 3)
Troco = 50 – 25,50
Troco = 24,50
D) Formando
equações algébricas:
Pense em um número, some cinco ao número, dobre o resultado,
subtrai 4, qual o reultado final?
Número = X
Soma
5 = x+5
Dobre
o resultado = 2.(x+5)
Subtrai 4 = 2.(x+5) – 4
Resultado final =
2.(X+5)-4=
(2.X) + ( 2.5) – 4 = multiplica por 2 para
eliminar o parêntese
2.X + 10 – 4
Para finalizar
Resolva agora os exercícios da apostila volume 4
7º ano
Pg 109 e Atividade 1.1; 1.2 e 1.3
Pg 110 Atividade 2.1; 2.2 e 2.3
Pg 111 Atividade 3.1 ; 3.2 ; 3.3
Pg 112 Atividade 4.1;
4.2; 4.3
Pg113 Atividade 5.1 ;
5.2; 5.3
Pg 114 Atividades 6.1; 6.2; 6.3; 6.4;
Atividade 2 - 4º Bimestre-
Geometria ----- Habilidade - (EF07MA27) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos.
Soma dos ângulos internos e externos de um polígono convexo
Considerando as diagonais traçadas por apenas um dos vértices de um polígono, é possível perceber que elas formam triângulos. Conforme aumentamos os lados de um polígono, a quantidade de triângulos também aumenta. Veja:
Em um quadrilatero , conseguimos formar dois triângulos.
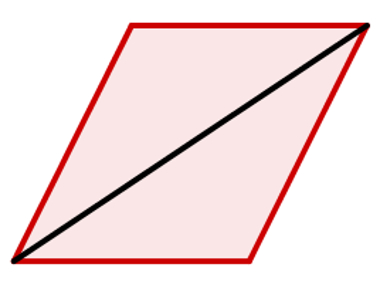
Considerando que, em cada triângulo, a soma dos ângulos internos iguais é 180°, a soma dos ângulos internos de qualquer quadrilátero é 2·180º = 360º.
Em um polígono de cinco lados (pentágono), formamos três triângulos.
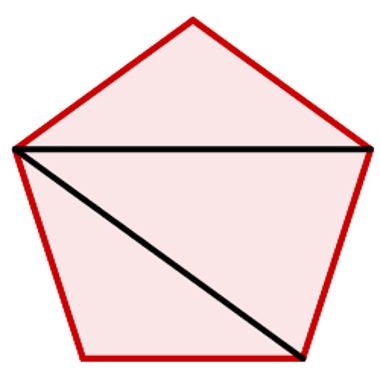
Dessa forma, temos que a soma dos ângulos internos de um pentágono é 180º·3 = 540º
Em um polígono de seis lados (hexágono), formamos quatro triângulos.
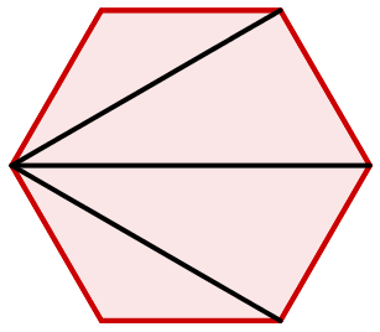
Portanto, a soma dos ângulos internos é 4·180º = 720º.
Soma dos ângulos internos de um polígono convexo
Percebemos que a diferença do número de triângulos formados e o número de lados dos polígonos é sempre 2, então, concluímos que:
n = 3
Si = (3 – 2)·180º = 1·180° = 180°
n = 4
Si = (4 – 2)·180° = 2·180° = 360°
n = 5
Si = (5 – 2)·180° = 3·180° = 540°
n = 6
Si = (6 – 2)·180° = 4·180° = 720°
n = n
Si = (n – 2)·180°
Portanto, a soma dos ângulos internos de qualquer polígono é calculada pela expressão:
Si = (n – 2)·180°
A soma dos ângulos externos de qualquer polígono convexo é igual a 360°.
Obs.: A soma de um ângulo interno com o seu respectivo externo é igual a 180º, isto é, eles são suplementares.
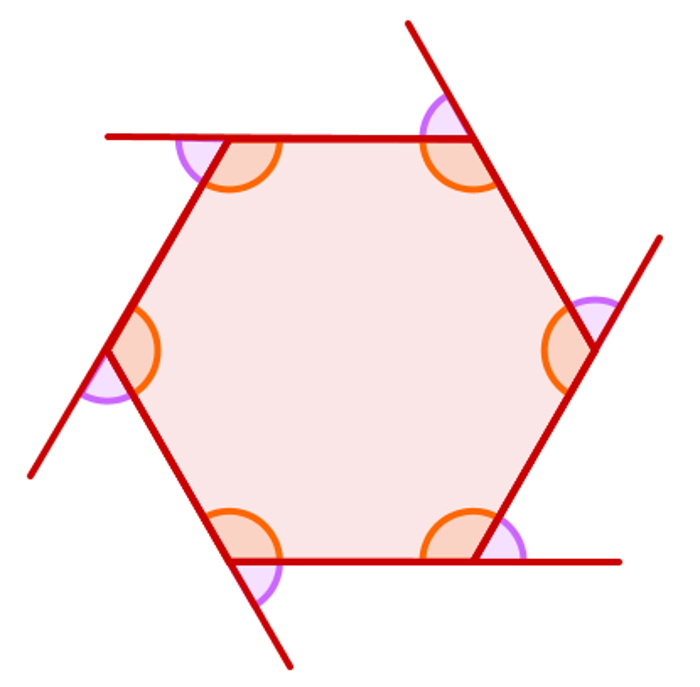
Fonte:
https://brasilescola.uol.com.br/matematica/soma-dos-angulos-internos-externos-um-poligono-convexo.htm
Vídeo soma dos ângulos externos
Resolver os exercícios Apostila
Apostila Matemática volume 4 - 7 ano --
Página 115 SITUAÇÃO DE APRENDIZAGEM 2
ATIVIDADE 1 – TRIÂNGULOS: MEDIDAS DE ÂNGULOS
ATIVIDADE 2: DECOMPOSIÇÃO DE POLÍGONOS EM TRIÂNGULOS pg116
ATIVIDADE 3 – POLÍGONOS REGULARES E ÂNGULOS INTERNOS pg117 e 118
ATIVIDADE 4 – POLÍGONOS REGULARES: ÂNGULOS INTERNOS E EXTERNOS pg 119
Atividade 3 - 4º Bimestre-
SEQUÊNCIA DIDÁTICA – GRANDEZAS E
MEDIDAS Habilidade - EF07MA31
(EF07MA31) Estabelecer expressões de cálculo de área
de triângulos e de quadriláteros.
Com base nas informações apresentadas no Quadro acima, responda as
questões a seguir.
1-Após apresentar o Quadro acima aos irmãos, pai Gonçalo perguntou, de que maneira eles poderiam organizar as informações, de modo que conseguissem calcular a área do quadrilátero. Notando que os irmãos estavam com dificuldade em responder, apresentou uma lista de opções e perguntou, qual delas não condiz com a verdade? Responda você também.
A) ( ) Sabendo que os triângulos têm a mesmas medidas e que juntas
apresentam um quadrilátero de medida igual ao azul da imagem,
basta calcular a área de um destes triângulos e multiplicar por 2
para saber a área do quadrilátero;
B) ( ) Sabendo que os triângulos são projeções transladadas dos
polígonos formados ao considerarmos a região delimitada pela
diagonal do quadrilátero e dois de seus lados, ao multiplicar a
medida da base deste triângulo que é reto pela medida do seu
lado (o que forma 90º com a base) e dividir o resultado por 2,
teremos sua área, então, basta multiplicar por dois que teremos
a área do quadrilátero;
C) ( ) Sabendo que os triângulos tem lados iguais a
do quadrilátero e que se ao juntarmos teremos um quadrilátero
igual ao que procuramos a medida, basta então juntar as figuras e
calcular a o produto da medida da base pela altura do novo quadrilátero;
D) ( ) Nenhuma das opções.
2-Com base nas afirmações anteriores (ou outras que você conseguir elaborar), queremos que você escreva uma expressão que atenda as afirmativas que nos permita calcular a área do quadrilátero utilizando apenas do triângulo em questão.
3-Olhando para os quadrados formado pela malha no fundo das
figuras geométricas, Vinícius percebeu que cada um dos quadrados
tinha área de 2 unidades de medida, por exemplo, se falamos de cm,
então cada quadradinho tem 2cm². Com base nesta constatação,
Vitória apresentou algumas afirmações e te perguntamos,
em qual delas Vitória se equivocou?
A) ( ) Se cada um dos quadradinhos tem área de 2cm²,
então se temos 3 de base e 3 de altura, basta multiplicar 3 x 3
que teremos a medida de área procurada;
B) ( ) Somando 3 quadradinhos inteiros e 3 pela metade em cada
triângulo, podemos encontrar o valor da área do quadrilátero;
C) ( ) Podemos dividir cada um desses quadradinhos em triângulos
de área 1cm², ai somamos todos os triângulos menores presente
nos dois triângulos maiores e identificamos a área total do quadrilátero;
D) ( ) Se multiplicarmos por 2 a medida identificada pelo produto
de quantidades dos quadradinho no quadrilátero, teremos a medida
de área procurada.
4-Vinícius percebeu que se dividirmos cada quadradinho desse
mencionado no exercício anterior, em quatro quadradinhos medindo
0,5cm², e perguntou a Vitória, quantos deles estarão presentes no
quadrilátero para cobrir toda a sua área?
5-Vitória que não é boba, lançou também um desafio a Vinícius,
ela notou que se cortarmos o quadrilátero azul pelas duas diagonais
, teremos nele representado quadro triângulos menores dos que
estes presentes na imagem do Quadro anterior, e perguntou a
Vinícius, qual seria a área em cm² de um destes novos triângulos?
6-Uma horta quadrada que Mãe Ana construiu, foi formada em um
terreno retangular, de 8 m por 12 m, conforme mostra a figura.
Mãe Ana agora deseja ladrilhar todo o terreno restante em volta
da horta.
A) Calcule a área da horta;
B) Calcule a área do terreno;
C) Calcule a área que será ladrilhada;
D) Os ladrilhos terão forma retangular, de 0,25 m por 0,5 m,
quantos ladrilho será necessários para ladrilhar essa área?
7-A calçada de entrada do mercadinho de mãe Ana está sendo
reformada. Serão feitas duas jardineiras triangulares e iguais
nas laterais, conforme indicado na figura, e o calçada restante
será revestido em cerâmica.
Qual a área do piso que será revestida com cerâmica?
SEQUÊNCIA DIDÁTICA – GRANDEZAS E
MEDIDAS Habilidade - EF07MA32
(EF07MA32) Resolver e elaborar problemas de
cálculo de medida de área de figuras planas que podem ser
decompostas por quadrados, retângulos e/ou triângulos,
utilizando a equivalência entre áreas.
Com base nas informações apresentadas no Quadro acima, responda
às seguintes questões.
1-As figuras do Quadro anterior apontam para o modelo de cerâmica
que pai Gonçalo estuda utilizar para cobrir uma área do novo
mercadinho (representada pelo quadrilátero azul). Ele sabe que o
palete de cerâmica de cor verde apresenta uma certa quantidade de
cerâmicas verdes e quadradas, tal que seria necessário 12 paletes
destes para cobrir toda a área desejada. Sabendo que cada cerâmica
do palete tem medida de 1m² e que o total de m² de cada palete é 25,
quantos metros quadrados tem a área a ser coberta?
2-Mãe Ana, prefere que a cerâmica a ser utilizada deva ser de cor
amarela. No entanto, sabendo que o palete tem 25 cerâmicas de
modelo inteiriço no formato retangular de 1m x 2m medindo 2m²,
quantos paletes de cor amarela Ana precisa ter para cobrir a área desejada?
3-Vinícius queria que metade da área fosse laranja e a outra metade fosse
roxa. Mantendo as proporções já levantadas nas atividades anteriores
(um palete laranja com peças neste formato com medidas de 3m² e
contendo 25 unidades, e um palete roxo com 25 unidades de cerâmica
no formato de triângulo reto de 0,5m²), ele quer saber, quantos paletes
serão necessários de cada cor?
4-Olhando para a figura onde todas as cerâmicas foram dispostas sobre
a área, Vitória percebeu que algumas áreas ainda ficaram sem cerâmica
(áreas em azul). Com base nesta constatação, responda, quais das
afirmações a seguir não indicam a quantidade correta de paletes
para cobrir estas áreas?
A) ( ) Dois paletes verdes são suficientes;
B) ( ) Um palete laranja (recortando algumas unidades) e
um roxo são suficientes; C) ( ) Dois paletes amarelo dão e sobram;
D) ( ) Um palete marrom dá conta.
5-Observando a área coberta pelo palete marrom, responda, quantos
serão necessários para cobrir a área azul?
6-No quarto de Vitória há uma parede em que cabem 26 cerâmicas
azuis no comprimento e 24 na altura. Para reformar essa parede,
qual a quantidade de cerâmica que Vitória vai precisar comprar?
7-A figura abaixo representa um terreno retangular que Vinícius quer
comprar, e uma casa quadrada que pretende construir dentro do terreno.
A). Qual a área do terreno?
B). Qual a área ocupada pela casa?
C). Qual a área do quintal?
SEQUÊNCIA DIDÁTICA – GRANDEZAS E MEDIDAS Habilidade - EF07MA33
(EF07MA33) Estabelecer o número π como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica.
Com base nas informações apresentadas no Quadro acima, responda as questões a seguir.
1-Após desenhar o perímetro do quiosque e a partir do centro dele riscar em linha reta até a circunferência para depois medir e descobrir o raio do círculo formado, mãe Ana decidiu que para ser um espaço bom, este raio deveria ter medida igual a 5 metros. Diante desta informação, e sabendo que a razão ideal entre a medida da circunferência deste círculo pela medida de seu diâmetro deve ser 31,4, qual a medida que a circunferência precisa ter?
2-Pai Gonçalo acha que uma circunferência com medida de 35m daria um raio interessantes para a construção do quiosque, no entanto, a razão dada pela divisão da circunferência pelo diâmetro deu um valor de 3,125 metros. Com estes dados em mãos, responda, qual a medida deste raio?
3-Assumindo as medidas apresentadas por pai Gonçalo, onde a medida da circunferência é 35m e o diâmetro igual a 11,2m, mãe Ana dividiu o círculo em 4 setores de mesma área, uma para cada banca de vendas. Agora, quer mandar fazer móveis planejados para a área, e precisa saber a medida do perímetro formado em cada setor. Com estas informações, responda, qual a medida do perímetro de cada um dos setores?
A) ( ) 19,95m;
B) ( ) 35m;
C) ( ) 22,8m;
D) ( ) 40,6m.
4-Sabendo que uma praça ali perto do mercadinho tem um canteiro com forma de uma circunferência de medida 60m e o raio desta circunferência medindo 5m, quanto será a medida de seu diâmetro e a razão da circunferência pelo diâmetro?
5-Mãe Ana, após desenhar todo o percurso da circunferência onde será construído as muretas que os cerca, resolveu medir a distância de um certo percurso, a iniciar sua saída do centro do círculo, caminhar em linha reta pelo raio até a circunferência, seguir em sentido anti-horário até dar uma volta completa na circunferência. Ao fazer isso, Ana percorreu uma distância equivalente à do raio mais a da circunferência. Sabendo desta informação e que a circunferência mede 35m e o diâmetro mede 11,2m, responda, qual a distância que mãe Ana percorreu? Esta distância é duas vezes maior que a distância da razão entre circunferência e o raio deste círculo?
6-Pai Gonçalo resolveu investir um bom dinheiro ganhou num sorteio da lotofácil realizado na loteria da Avenida Mato – Grosso no bairro Cidade Nova, juntamente com suas outras economias. Comprou um terreno ao lado do mercadinho de mãe Ana e nele resolveu construir em uma determinada área uma lanchonete, além de uma piscina adulta e outra infantil, ambas cobertas. Como o seu terreno é bem
amplo, mãe Ana deu a ideia para ele de construir também 5 quiosques com churrasqueiras, pias e mesas de mármore para atender melhor seus clientes. Sendo Gonçalo uma pessoa muito simples perguntou a sua esposa como ela gostaria que o formato dos quiosques? Qual o tamanho ideal para comportar os 5 quiosques no espaço mantendo uma boa distância um do outro? Seria no formato quadrangular, ou circular? Será que o espaço será suficiente?
Mae Ana, que entende bem de matemática, disse que já estava com tudo em mente, afirmando a Gonçalo que o formato deveria ser circular e que as circunferências deveriam ter exatamente 10 metros de diâmetro cada e 31,4 metros de comprimento conforme algumas medições que a mesma já havia realizado da área a ser construída. Em seguida Ela mostrou a ele o desenho inicial feito em seu computador.
Vamos ter que usar aquela fórmula que fala do tal do π (pi) Ana (perguntou Gonçalo)? Depois você me explica o que exatamente significa esse tal do π? Com base nas informações contidas no desenho feito por Ana, como ela já havia calculado a medida do comprimento de cada circunferência, ao dividirmos o comprimento da circunferência de um dos quiosques pelo seu diâmetro encontramos aproximadamente qual valor? Ajude a responder.
7-Muito curioso, pai Gonçalo questionou mãe Ana se ela saberia dizer que se sabendo a medida do diâmetro, qual seria o tamanho da área de cada circunferência e a área total de todas essas circunferências para poder comprar os azulejos para todos os quiosques. Mãe Ana está em dificuldades, você poderá a ajudar? Responda à pergunta de pai Gonçalo.
Resolver os exercícios da apostila volume 4 -- 7º Ano
Página 124 ---- SITUAÇÃO DE APRENDIZAGEM 4 ATIVIDADE 1 – MEDIDAS DAS ÁREAS DO RETÂNGULO E DO QUADRADO
No gráfico de setores, os dados percentuais são distribuídos conforme a proporção da área a ser representada.
Atualmente a Matemática dispõe de ferramentas tecnológicas no intuito de dinamizar os cálculos e as representações gráficas. Quanto aos gráficos podemos utilizar programas específicos na sua elaboração, o Excel e o Calc são ferramentas muito utilizadas nesse sentido, mas as representações gráficas também podem ser produzidas de forma artesanal. A seguir demonstraremos como construir um gráfico de setores ou de pizza, como muitos o denominam.
Para representar os dados em um gráfico de setores é preciso que os valores estejam em porcentagem, para isso devemos definir a frequência relativa dos dados observados. Vamos trabalhar com o seguinte modelo de exemplo:
Uma escola realizou uma pesquisa com seus 400 alunos do Ensino Médio sobre a preferência por modalidades esportivas. Os dados foram distribuídos em uma tabela, veja:.jpg)
FA: frequência absoluta
FR: frequência relativa
Como o gráfico é de setores, os dados percentuais serão distribuídos levando-se em conta a proporção da área a ser representada relacionada aos valores das porcentagens. A área representativa no gráfico será demarcada da seguinte maneira:
.jpg)
Concluímos que 1% corresponde a 3,6º, dessa forma podemos calcular os ângulos dos dados percentuais da seguinte maneira:
.jpg)
Para construir o gráfico esboçamos uma circunferência marcando o seu raio, e, com o auxílio do transferidor, traçamos um ângulo com vértice no centro da circunferência, relativo à primeira porcentagem.
.jpg)
Em seguida, ao marcar o próximo ângulo, devemos considerar o raio traçado, referente à porcentagem anterior, como um dos seus lados e o centro da circunferência como seu vértice. Repita o procedimento até que todos os ângulos sejam marcados. Vale lembrar que o centro da circunferência será o vértice de todos os ângulos. Feita a marcação dos ângulos, basta pintar os setores, fazer a anotação das porcentagens e construir uma legenda. Observe o gráfico pronto:
.jpg)
Média
Média (M), mais precisamente chamada de média aritmética simples, é o resultado da soma de todas as informações de um conjunto de dados dividida pelo número de informações que foram somadas. A média aritmética simples entre 14, 15 e 25, por exemplo, é a seguinte:
M = 14 + 15 + 25
3
Como há três dados na lista, dividimos a soma desses dados pelo número 3. O resultado é:
M = 54
3
M = 18
A média é a medida de centralidade mais usada por ser a que mescla de maneira mais uniforme os valores mais baixos e os mais altos de uma lista. No conjunto anterior, por exemplo, a mediana é igual a 44,5, mesmo com tantas idades próximas de 20 anos. Observe a média aritmética simples desse mesmo conjunto:
M = 18 + 19 + 19 + 22 + 44 + 45 + 46 + 46 + 47 + 48
10
M = 35,4 anos



Cadê as respostas da pergunta
ResponderExcluirPode me falar a resposta da 5
ResponderExcluirCadê o gabarito???? Se tivesse iria me ajudar muito!!!
ResponderExcluirKdr a respostas?
ResponderExcluir