professorcarlosribeiro@yahoo.com
Habilidade EF08MA02
Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
Objetos de Conhecimento
Potenciação e radiciação
Potências
MATEMÁTICA
A operação de potenciação com expoente natural pode ser interpretada como uma multiplicação com fatores iguais. Podemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 26, onde 2 é a base e 6 o expoente (Leia: dois elevado a sexta potência). Ou seja o 2 se repete 6 vezes.
Exercício 1) Escreva as multiplicações em forma de potências.a) 2x2x2x2x2= b)3x3x3x3x3x3x3x3=c)10x10x10x10=
Exercício 1) Escreva as multiplicações em forma de potências.a) 2x2x2x2x2= b)3x3x3x3x3x3x3x3=c)10x10x10x10=
A operação efetuada é denominada potenciação.
Exemplos:
54 = 5 . 5 . 5 . 5 = 625
43 = 4 . 4 . 4 = 64
Exercício 2 -Escreva na forma de multiplicação cada uma das seguintes potências e de o resultado:
a) 112 ______11x11=121__
b) 73 ___________________
c) 84 ___________________
d) 36 ____________________
e) 27 ____________________
a) 34 = ___3x3x3x3=81_____3x3=9x3=27x3=81
b) 24 = __________________
c) 100 = ___ 1____________
d) 203 = __________________
e) 1001 = __100__________
f) 28 = ___________________
g) 53 = ___________________
Execício 4) Resolver as potências com expoente negativo.
-3
a)5 =
-4
b)3 =
-6
c)2 =
-4
b)3 =
-6
c)2 =
Potências de frações

Como exemplo, vamos determinar o resultado da potência a seguir:

Frações com expoente negativo
Quando o expoente de uma fração é negativo, devemos fazer o seguinte para possibilitar os cálculos:
- Escrever a base em forma de fração se ela ainda não estiver nessa forma;
- Inverter a base e o sinal do expoente;
- Usar a propriedade das potências de fração relembrada acima.
Matematicamente, essa propriedade é escrita da seguinte maneira:

Exemplos
1º caso:
Use os três passos descritos acima para resolver esse exemplo: transforme a base em fração, inverta a base e o sinal do expoente e utilize a propriedade da potência de fração:

2º caso:

Para resolver esse exercício, faça como no anterior:

Exercício 5 Resolver as potências das frações com expoente negativo
-3 -4 -2
a)(2/5) b)(3/4) c)(4/5)
Propriedade das potências
Propriedade 1. Multiplicação de potências com bases iguais.
a) 72 x 73 = (7 x 7) x (7 x 7 x 7) = 7 x 7 x 7 x 7 x 7 = 75
b) 24 x 23 x 22 = (2 x 2 x 2 x 2) x (2 x 2 x 2) x (2 x 2) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 29
Observando os dois exemplos acima, temos que:
72 x 73 = 72+3 = 75
24 x 23 x 22 = 24+3+2 = 29
Essa propriedade nos mostra que: na multiplicação de potências de bases iguais basta conservar a base da potência e somar os expoentes. Observe novamente:
35 x 38 = 35+8 = 313
a) 72 x 73 = (7 x 7) x (7 x 7 x 7) = 7 x 7 x 7 x 7 x 7 = 75
b) 24 x 23 x 22 = (2 x 2 x 2 x 2) x (2 x 2 x 2) x (2 x 2) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 29
Observando os dois exemplos acima, temos que:
72 x 73 = 72+3 = 75
24 x 23 x 22 = 24+3+2 = 29
Essa propriedade nos mostra que: na multiplicação de potências de bases iguais basta conservar a base da potência e somar os expoentes. Observe novamente:
35 x 38 = 35+8 = 313
Propriedade 2. Divisão de potências com bases iguais.
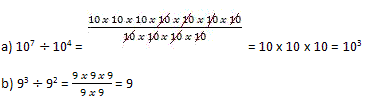
Com os exemplos acima, pode-se verificar que:
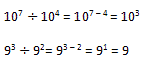
Essa propriedade nos mostra que: na divisão de potências com bases iguais basta conservar a base e diminuir os expoentes. Veja:
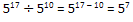
Propriedade 3. Potência de potência
Essa propriedade é chamada de potência de potência por apresentar uma base com dois ou mais expoentes.
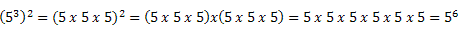
Essa propriedade é chamada de potência de potência por apresentar uma base com dois ou mais expoentes.
Com o exemplo acima, podemos verificar que:
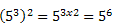
Essa propriedade nos mostra que: numa potência de potência devemos repetir a base e multiplicar os expoentes. Veja:
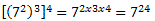
Propriedade 4. Potência com expoente zero.
Essa é uma propriedade muito interessante e que gera muita dúvida nas pessoas. Ela nos diz que todo número elevado a um expoente zero terá como resultado o número 1. De forma genérica seria:
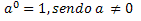
Essa é uma propriedade muito interessante e que gera muita dúvida nas pessoas. Ela nos diz que todo número elevado a um expoente zero terá como resultado o número 1. De forma genérica seria:
Vejamos mais um exemplo:
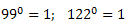
Mas como podemos chegar a essa conclusão? Por que todo número elevado a zero é igual a 1?
Veja como é simples a explicação disso. Vamos fazer a divisão entre os números abaixo:
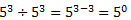
Mas como todo número dividido por ele mesmo resulta 1, temos que:
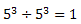
Veja como é simples a explicação disso. Vamos fazer a divisão entre os números abaixo:
Mas como todo número dividido por ele mesmo resulta 1, temos que:
Com as duas igualdades, podemos concluir que:
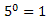
Exercício 6-Resolver utilizando as propriedades das potências:
3 4
a)7 x 7 =
5 3
b)5 x 5 =
10 5
c)7 x 7 =
5 3
b)5 x 5 =
10 5
c)7 x 7 =
9 6
Fração como expoente
MATEMÁTICA
Ao nos depararmos com uma fração como expoente, podemos transformá-la em uma raiz.
O expoente está relacionado com o cálculo da potenciação. A potência de um número é determinada pela fórmula descrita a seguir
an = c
a = base; n = expoente; e c = potência.
a = base; n = expoente; e c = potência.
Exemplos:
23 = 2 . 2. 2 = 8 → a = 2, n = 3 e c = 8
52 = 5 . 5 = 25 → a = 5, n = 2 e c = 25
52 = 5 . 5 = 25 → a = 5, n = 2 e c = 25
Quando esse expoente é uma fração, ou seja, possui numerador e denominador, devemos transformá-lo em uma raiz, isto é:
.jpg)
No lado esquerdo da igualdade, temos que: a = base, n = expoente.
m
m
Já no lado direito da igualdade: a = radicando, m = índice e n = expoente.
Nessas transformações do expoente fracionário em radiciação, vale a recíproca, ou seja:
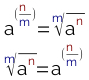
Para compreender melhor como transformamos o expoente fracionário em raiz, veja como foram solucionados os exemplos a seguir:
Exemplos:
1) Transforme as raízes a seguir em expoentes fracionários com base:
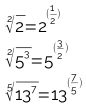
2) Transforme os expoentes fracionários em raízes:
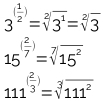
3) Efetue o produto e encontre a solução da seguinte expressão:
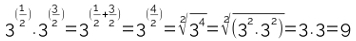
B)Transforme os expoentes fracionários em raízes
Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Objetos de Conhecimento
O princípio multiplicativo da contagem
O princípio multiplicativo da contagem
Princípio fundamental da contagem
A analise combinatória é utilizada para resolver problemas de contagem. Utilizando os processos combinatórios é possível determinar o número de combinações, arranjos e permutações possíveis. Para cada uma destas aplicações, alguns critérios devem ser respeitados. Iremos agora conduzir você a entender o Diagrama da Árvore. Quando conseguir assimilar esta estrutura será fácil entender o Princípio Fundamental da Contagem, que define - se como sendo:
Em notação matemática isso seria o mesmo que considerarmos, que determinada atividade pode ser realizada em duas etapas, ou seja, de m e n maneiras distintas, o total de possibilidades será dado pelo produto de m por n (m x n). Iremos agora resolver um problema utilizando o Diagrama da Árvore para que possamos entender o Princípio Fundamental da Contagem:
Problema: Jeniffer irá participar da promoção de uma loja de roupas que está dando um vale compras no valor de R$ 1000,00 reais. Ganhará o desafio o primeiro participante que conseguir fazer o maior número de combinações com o kit de roupa cedido pela loja. No kit temos: seis camisetas, quatro saias e dois pares de sapato do tipo salto alto. De quantas maneiras distintas Jeniffer poderá combinar todo o vestuário que esta no quite de roupa?
Peças que compõem o kit de roupa
Camisetas

Saias

Sapatos

Utilizando o Diagrama da Árvore vamos descobrir a quantidade de combinações possíveis.

8 combinações possíveis.
| 
8 combinações possíveis.
|

8 combinações possíveis.
| 
8 combinações possíveis.
|

8 combinações possíveis.
| 
8 combinações possíveis.
|
Ao realizar a contagem iremos constatar a quantidade referente à 48 combinações possíveis.
A outra forma que temos para resolver este problema é utilizando o Princípio Fundamental da Contagem.
Total de camisetas X Total de Saias X Total Sapatos = Total de combinações possíveis
6 x 4 x 2 = 48
Observe que ao utilizarmos o Princípio Fundamental da Contagem, também foi possível determinar o número de combinações do Kit roupa, este número corresponde ao que foi encontrado quando utilizamos o Diagrama da árvore.
Resolva as seguintes situações problemas
1- Um homem vai a um restaurante disposto a comer um só prato de carne e uma só sobremesa. O cardápio oferece oito pratos distintos de carne e cinco pratos diferentes de sobremesa. De quantas formas pode o homem fazer sua refeição.
2-Uma moça possui 5 blusas e 6 saias. De quantas formas ela pode vestir uma blusa e uma saia?
3- Um homem possui 10 ternos,12 camisas e 5 pares de sapato. De quantas formas poderá vestir 1 terno, 1 camisa e 1 par de sapato?
4-De quantas maneiras podemos escolher um chefe, um tesoureiro e um secretário para um clube, sendo que há 10 candidatos a chefe, 20 candidatos a tesoureiro e 30 candidatos a secretário?
5-De quantas maneiras podemos escolher um capitão, um imediato e um cozinheiro de bordo de uma tripulação composta por 15 homens?
Observação exercício 5: ▸ Há 15 possibilidades de escolha para o capitão.
▸ Escolhido o capitão, há 14 possibilidades de escolha para o imediato.▸ Selecionado este último, sobram 13 homens para a escolha do cozinheiro de bordo.
Habilidades EF08MA04
Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
Objetos de Conhecimento
Porcentagens
Índice percentual
Toda razão cujo denominador é igual a 100 é chamada de índice percentual.
A porcentagem é um conteúdo da matemática financeira utilizado para calcular: rendimento, taxa de juros, capitalização, empréstimos, aplicações, desconto, índices de inflação (aumento persistente no valor dos preços) e índices de deflação (queda de preços constante).
A unidade fundamental da porcentagem é dada por este símbolo: %, que significa “por cento”, essa palavra tem a sua origem no latim “per centum”, que significa “por um cento”.
Para tratarmos de índice percentual precisamos entender o que é razão. Razão nada mais é que uma divisão na estrutura de fração, que possui numerador e denominador. Já razão centesimal é toda fração cujo denominador é o número 100, quando a razão é desse tipo é chamada de índice ou taxa percentual. Logo podemos concluir que:
Taxa Percentual = Índice Percentual = Razão centesimal
Quando a = a → Sendo b = 100
b 100
b 100
Para entender melhor o que é índice percentual observe o exemplo abaixo:
Exemplo 1
Represente 35% na forma de índice percentual, em seguida faça a sua representação decimal.
Resposta:
35% = 35 = 0,35
100
100
Onde: 35% → Representação percentual
85 → Razão centesimal ou Índice Percentual.
100
100
0,35 → Representação decimal.
Vamos agora aplicar o conteúdo referente à índice percentual em algumas situações:
Exercício 9
Represente as percentagens na forma de índices percentual
A)45%
B)35%
C)48%
D)55%
E)59%
F) Considere que 85,5% da população do Brasil possui celular.Escreva esse valor em forma de índice percentual.
Como calcular porcentagem de um valor?
Para saber o percentual de um valor basta multiplicar a razão centesimal correspondente à porcentagem pela quantidade total.
Exemplo: para descobrir quanto é 20% de 200, realizamos a seguinte operação:
20% de 200 =
20/100 x 200 =
0,2 x 200= 40
Exercício 10
Descubra o valor percentual dos seguintes valores:
A)10% de 500
B)25% de 350
C)35% de 700
D) 40% de R$ 5000,00
E) 90% de R$ 3500,00
Exercício 11
Resolver as seguintes situações problema de porcentagem:
A) Em um determinado vestibular, 25% dos candidatos faltaram no dia da prova. Se o total de inscritos era 150.000 candidatos, quantos candidatos faltaram?
exercício resolvido
Devemos calcular 25% de 150.000
25/100 x 150.000 =
0,25 x 150.000 =
37.500
C) Uma determinada loja de eletrônicos esta colocando produtos a venda com os seguintes descontos. Um celular que custa R$ 950,00 foi oferecido com 15% de descontos se for pago a vista e 8% de desconto se for pago a prazo. Qual o valor do celular se for pago a vista? E se for pago a prazo?
D) Achando a porcentagem dados 2 valores.
Exercício resolvido
Em uma escola foi feita uma pesquisa com 600 alunos, dos quais 162 alunos responderam que preferem amigos virtuais, qual o porcentagem de alunos preferem amigos virtuais?
Devemos multiplicar a parte dos alunos 162 por 100 e dividir por 600 que é o total, para achar a porcentagem.
Exercício resolvido
162x100 / 600=
16.200 / 600=
27 %
E) Em uma escola foi feita uma pesquisa com 600 alunos, dos quais 330 responderam que preferem amigos virtuais, qual a porcentagem de alunos que preferem amigos virtuais?
F)Em uma escola foi feita uma pesquisa com 600 alunos, dois quais 108 disseram passar mais de 3 horas nas redes sociais diariamente, qual a porcentagem de alunos que passam mais de 3 horas nas redes sociais?
G) Um reservatório de 1000 litros, esta com a capacidade de 600 litros preenchido com gasolina. Qual a porcentagem esta preenchida com gasolina? E qual a porcentagem da capacidade que não esta preenchida?
Habilidades EF08MA15
Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.
Objetos de Conhecimento
Construções geométricas: ângulos de 90°, 60°, 45° e 30° e polígonos regulares
Assista o vídeo acima e execute as seguintes tarefas
1- Construa um segmento AB = 5 centímetros e trace a mediatriz desse segmento.
2- Construa um segmento OA de 8 centímetros, e marque os pontos O e A ,depois com o transferidor construa um angulo de AÔB = 60º Por fim Trace a bissetriz desse ângulo.
3- Usando o mesmo processo do exercício 2 trace a bissetriz dos seguintes ângulos
BÔD = 30º
XÔY = 45º
EÔF = 90º
Habilidades EF08MA16
Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.
Objetos de Conhecimento
Construções geométricas: ângulos de 90°, 60°, 45° e 30° e polígonos regulares
Exercício 13
Assista o vídeo acima e construa um Hexágono regular de lado 50 milímetros ou 5 centímetros
Habilidades EF08MA14
Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetos de Conhecimento
Congruência de triângulos e demonstrações de propriedades de quadriláteros

.jpg)
Retângulo: apresenta ângulos retos e diagonais congruentes
.jpg)
O losango possui diagonais perpendiculares
.jpg)
Exemplo de trapézio isósceles

Retângulo, paralelogramo e trapézio
Definição: Congruência de triângulos
Quadriláteros são polígonos que possuem quatro lados. Suas características e propriedades específicas dizem respeito aos seus lados, ângulos e diagonais.
Quadriláteros são polígonos que possuem quatro lados. Sendo assim, os quadriláteros herdam todas as características e propriedades dos polígonos, como o fato de possuírem apenas duas diagonais ou de a soma de seus ângulos internos ser sempre igual a 360°.
Elementos de um quadrilátero
- Lados: São os segmentos de reta que contornam o quadrilátero;
- Vértices: São os pontos de encontro entre dois lados;
- Ângulos internos: São os ângulos determinados por dois lados consecutivos de um quadrilátero;
- Ângulos externos: são ângulos formados pelo prolongamento de um lado de um polígono. Um ângulo externo sempre é suplementar ao ângulo interno adjacente a ele;
- Diagonais: Segmentos de reta cujas extremidades são dois vértices não consecutivos de um polígono. Dessa maneira, são os segmentos de reta que ligam dois vértices e que, ao mesmo tempo, não são lados.

Um quadrilátero é convexo quando está completamente em um dos semiplanos formados pela reta que resulta do prolongamento de um de seus lados.
Classificação de quadriláteros
Os quadriláteros podem ser classificados de acordo com a posição relativa entre seus lados. Aqueles que possuem lados opostos paralelos são chamados de paralelogramo. Os quadriláteros que possuem um par de lados opostos paralelos e outro não são chamados de trapézios. A terceira classe dos quadriláteros contém aqueles que não possuem paralelismo algum entre seus lados.
Paralelogramos
Os paralelogramos possuem uma característica a mais que os quadriláteros, que é o fato de possuírem lados opostos paralelos. Isso acarreta uma série de propriedades pertencentes somente a eles.
- Possuem lados opostos congruentes;
- Possuem ângulos opostos congruentes;
- Possuem ângulos adjacentes suplementares;
- As diagonais de um paralelogramo cruzam-se em seus pontos médios.
Existe uma classificação para os paralelogramos em retângulos , losangos, quadrados ou nenhum deles.
Retângulo
Os retângulos são paralelogramos cujos ângulos internos são retos (daí o nome retângulo). Eles possuem todas as características dos paralelogramos e uma propriedade específica, a saber:
“As diagonais de um retângulo são congruentes.”
.jpg)
Retângulo: apresenta ângulos retos e diagonais congruentes
Losango
Os losangos são paralelogramos que possuem todos os lados congruentes, isto é, são paralelogramos equiláteros. Sua propriedade específica é a seguinte:
“As diagonais de um losango são perpendiculares.”
.jpg)
O losango possui diagonais perpendiculares
Quadrado
Os quadrados são losangos e retângulos simultaneamente e, por isso, possuem todos os ângulos retos e todos os lados congruentes. Sua propriedade específica é a seguinte:
“As diagonais do quadrado são perpendiculares e congruentes.”
Trapézios
Diferentemente dos paralelogramos, os trapézios possuem apenas um par de lados paralelos. Esses lados são chamados de bases. Os trapézios que possuem os outros dois lados que não são bases congruentes são chamados de isósceles.
.jpg)
Exemplo de trapézio isósceles
As propriedades específicas do trapézio isósceles são:
“Os ângulos da base e as diagonais são congruentes”.
Os trapézios possuem as mesmas características e propriedades dos quadriláteros, uma vez que não são paralelogramos.

Retângulo, paralelogramo e trapézio
Definição: Congruência de triângulos
Um triângulo é congruente (símbolo ) a outro se, e somente se, é possível estabelecer uma correspondência entre seus vértices de modo que:
- seus lados são ordenadamente congruentes aos lados do outros;
- seus ângulos são ordenadamente congruentes aos ângulos do outro.
Triângulo ABC congruente triângulo EFG
Exercício 14
Exercício resolvido
A) Na figura as retas F e G são paralelas e M é o ponto médio do segmento AD
Pode-se afirmar que o triângulo MAB e MCD são congruentes pelo caso
a) AAA b) ALA c) LAL d) LLL
B) Considerando ED congruente ST. Na figura abaixo para que os triângulos DEF e SUT sejam congruentes, os valores de x e Y devem ser ?
Se (Sobrepormos) ou seja colocarmos uma figura sobre a outra o lado ED ficara sobre o lado ST pois são congruentes
Logo ED=ST EF=SU DF=UT
EF=SU
EF = 5 SU = 2.x+1
5= 2.x+1
5-1 = 2.x
4 = 2.x
4/2 = x
2 = x ou seja x = 2
DF = UT
DF = y-5 UT = 3
y-5 = 3
y= 3+5
Y=8
ou seja y = 8
ou seja y = 8
C) A soma dos ângulos internos de um quadrilátero é 360º. Qual o valor de x no quadrilátero abaixo.
D) Considerando PQ congruente a ST . Na figura abaixo para que os triângulos PQR e STU sejam congruentes os valores de a e b devem ser?
Habilidades EF08MA22
Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Objetos de Conhecimento
Princípio multiplicativo da contagem
Soma das probabilidades de todos os elementos de um espaço amostral
Assista o vídeo introdução a Probabilidade
Assista o vídeo introdução a Probabilidade
Exemplos exercícios:
1) Marcos vendeu uma rifa com 100 números, dos quais Marcela comprou 15 números. Qual a Probabilidade de Marcela ser sorteada.
Espaço Amostral (E) = {100 números}
Evento (A) = { ser sorteado comprando 15 números}
Probabilidade (A) = números elementos do evento (A) / número elementos espaço amostral (E)
P(A) = N(A) / N(E)
P(A) = 15/100
P(A) = 0,15 x 100 = 15%
2) Uma urna contém 20 bolas pretas e 10 bolas Brancas. Qual a probabilidade de pegar uma bola ao acaso e ela ser branca?
Espaço amostral (E ) = { 10+20= 30 bolas}
Evento A = { ser branca = 10}
P(A) = N(A) / N(E)
P(A) = 10/30
P(A) = 0,3333 x 100= 33,3 %
Exercício 15
A- No lançamento de um dado qual a probabilidade de se obter um número menor que 5?
B- A probabilidade de se obter cara no lançamento de uma moeda é?
C- Priscila participou de um sorteio de um celular em que dos 500 bilhetes confeccionados para esse sorteio ela comprou 35 bilhetes. Qual a probabilidade de Priscila ser sorteada?
D- Em uma caixa há 8 bolas azuis, 10 vermelhas e 5 verde. Qual a probabilidade de se tirar ao acaso uma bola vermelha dessa caixa?
E- No lançamento de um dado qual a probabilidade de se obter um número par?
16 Exercício Diversos
A) Uma tanque de água tem capacidade de 1000 litros. Qual a porcentagem de água terá no tanque quando ele tiver 200 litros.
200/1000=0,2 x 100 = 20%
B) Calcule o valor a da expressão numérica:
(-3)² + 8.4 - 4.4 =
= +9 + 32 -16
= +41 - 16
= + 25
Observação: (-3)² = (-3) x (-3) = = +9
regra sinal multiplicação ( + ) . (+) = ( + )
( - ) . ( - ) = ( + )
( + ) . ( - ) = ( - )
( - ) . ( + ) = ( - )
C) Uma caixa de água tem capacidade de armazenar 500 litros. Neste momento ele esta armazenando 200 litros. Qual a porcentagem de água acumulada neste momento?
D) Calcule o valor da expressão numérica:
( - 9 ) ² + 5.7 - 3.4 =
Fontes de pesquisa:
http://matemagica.rio.br/blog/bncc/item/162-ef08ma01-matematica-8-ano-numeros.html
D) Calcule o valor da expressão numérica:
( - 9 ) ² + 5.7 - 3.4 =
Fontes de pesquisa:
http://matemagica.rio.br/blog/bncc/item/162-ef08ma01-matematica-8-ano-numeros.html
https://mundoeducacao.bol.uol.com.br/matematica/quadrilateros.htm
https://pt.slideshare.net/andreiarsz/mat-2-matutino-8-ano
https://brasilescola.uol.com.br/matematica/propriedades-das-potencias.htm
https://matematicabasica.net/potenciacao/
https://www.infoescola.com/matematica/principio-fundamental-da-contagem/
https://pt.slideshare.net/andreiarsz/mat-2-matutino-8-ano
https://brasilescola.uol.com.br/matematica/propriedades-das-potencias.htm
https://matematicabasica.net/potenciacao/
https://www.infoescola.com/matematica/principio-fundamental-da-contagem/
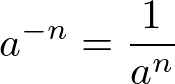
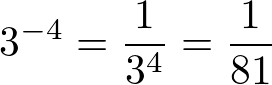
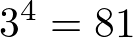
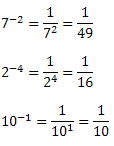











Essa lição foi difícil pra fazer
ResponderExcluir