8º ANO 3º BIMESTRE
OBJETOS DE CONHECIMENTO
Valor numérico de expressões algébricas.
Álgebra.
HABILIDADES
(EF08MA06) Resolver e elaborar situações-problema que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
03/08 - 8º ano EF - Matemática - Monômios e suas operações: Parte I
04/08 - 8º ano EF - Matemática - Monômios e suas operações: Parte II
05/08 - 8º ano EF - Matemática - Expressões algébricas: Parte III
10/08 - 8º ano EF - Matemática - Contexto algébrico e geométrico: Parte IV






11/08 - 8º ano EF - Matemática - Equações com duas incógnitas: PARTE I
12/08 - 8º ano EF - Matemática - Equação linear no plano cartesiano: Parte II
17/08 - 8º ano EF - Matemática - Resultados de uma equação de 1º grau com duas incógnitas: Parte III
18/08 - 8º ano EF - Matemática - Soluções de uma equação de 1º grau com duas incógnitas: Parte IV
19/08 - 8º ano EF - Matemática - Sistemas de duas equações com duas incógnitas: Parte I
31/08 - 8º ano EF - Matemática - Sistemas de duas equações com duas incógnitas: Parte II
01/09 - 8º ano EF - Matemática - Sistemas de duas equações com duas incógnitas: Parte III
02/09 - 8º ano EF - Matemática - Sistema de equações: Resolução gráfica: Parte IV
Um sistema de equações é constituído por um conjunto de equações que apresentam mais de uma incógnita. Para resolver um sistema é necessário encontrar os valores que satisfaçam simultaneamente todas as equações.
Um sistema é chamado do 1º grau, quando o maior expoente das incógnitas, que integram as equações, é igual a 1 e não existe multiplicação entre essas incógnitas.
Como resolver um sistema de equações do 1º grau?
Podemos resolver um sistema de equações do 1º grau, com duas incógnitas, usando o método da substituição ou o da soma.
Método da substituição
Esse método consiste em escolher uma das equações e isolarmos uma das incógnitas, para determinar o seu valor em relação a outra incógnita. Depois, substituímos esse valor na outra equação.
Desta forma, a segunda equação ficará com uma única incógnita e, assim, poderemos encontrar o seu valor final. Para finalizar, substituímos na primeira equação o valor encontrado e, assim, encontramos também o valor da outra incógnita.
Exemplo
Resolva o seguinte sistema de equações:
Resolução
Vamos começar escolhendo a primeira equação do sistema, que é a equação mais simples, para isolar o x. Assim temos:
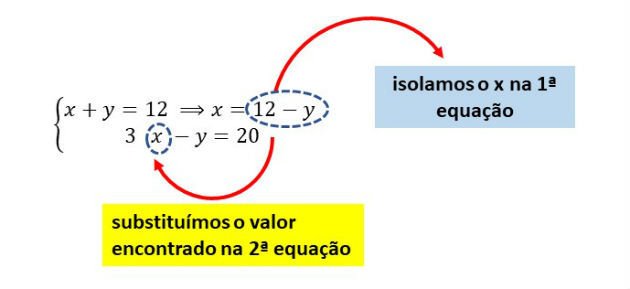
Após substituir o valor de x, na segunda equação, podemos resolvê-la, da seguinte maneira:
Agora que encontramos o valor do y, podemos substituir esse valor da primeira equação, para encontrar o valor do x:
Assim, a solução para o sistema dado é o par ordenado (8, 4). Repare que esse resultado tornam ambas as equações verdadeiras, pois 8 + 4 = 12 e 3.8 - 4 = 20.
Exercício 6
Resolver os seguintes sistemas pelo método da substituição.
Método da adição para sistemas com duas equações e duas incógnitas
método da adição. Ele visa a eliminar uma das incógnitas de um sistema pela soma dos termos semelhantes das equações que o compõem. No exemplo a seguir, observe que a simples soma dos termos das equações já zera uma das suas incógnitas:
incógnitas:
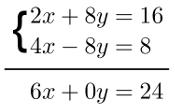
As somas realizadas nesse exemplo foram: 2x + 4x, 8y + (– 8y) = 0 e 16 + 8 = 24. Observe que, pelo resultado da soma, podemos encontrar o valor numérico de uma das incógnitas do sistema:
6x = 24
x = 24
6
x = 4
Para descobrir a incógnita y, basta substituir o valor numérico de x em uma das duas equações do sistema:
2x + 8y = 16
2·4 + 8y = 16
8 + 8y = 16
8y = 16 – 8
8y = 8
y = 8
8
y = 1
A solução desse sistema é S = {4, 1}.
Quando a soma dos termos não zera uma das incógnitas
O sistema do exemplo anterior foi resolvido com facilidade porque foi criado com os coeficientes da incógnita y opostas aditivas. Sempre que isso acontecer para uma das incógnitas, o método da adição é o mais indicado, pois os resultados são encontrados com muito mais agilidade.
Quando as incógnitas não forem opostas aditivas, ou seja, quando não forem o mesmo número com sinais diferentes, é necessário fazer um procedimento antes de somar as duas equações para que uma das incógnitas seja eliminada.
Para compreender esse procedimento, observe o exemplo a seguir:
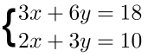
Observe que não é possível eliminar nenhuma das incógnitas, pois a soma das equações é:
5x + 9y = 28
Para viabilizar a eliminação de uma incógnita, devemos multiplicar uma das equações por uma constante para que pelo menos uma de suas incógnitas torne-se o inverso aditivo de uma das incógnitas da outra equação.
No exemplo, multiplicaremos a segunda equação por – 2. Esse valor foi escolhido para que o termo 3y tenha como resultado – 6y, que é o inverso aditivo de 6y da outra equação. Assim, é possível somar as duas, eliminando a incógnita y nesse processo.
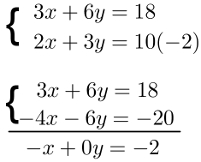
Observe que, ao multiplicar uma das equações por uma constante, todos os seus termos devem ser multiplicados por essa constante. Após a multiplicação, o sistema fica pronto para que a soma entre as equações seja feita. O resultado dessa soma é o seguinte:
– x = – 2
x = 2
Com o valor de uma das incógnitas, basta substituí-lo em uma das equações do sistema para descobrir o valor da outra incógnita:
3x + 6y = 18
3·2 + 6y = 18
6 + 6y = 18
6y = 18 – 6
6y = 12
y = 12
6
y = 2
A solução do sistema é S = {2, 2}
Exercício 7
Resolver os sistemas pelo método da adição:
Representando a idade de Lúcio por L e a de Joaquim por J, podemos construir as seguintes equações:
J + L = 60 e
J = 3L
Com essas duas equações, é possível montar o sistema a seguir, que será resolvido pelo método da comparação:
Sabendo que a idade de Lúcio é 15 anos e que a idade de Joaquim é o triplo da idade de Lúcio, teremos:
J = 3L
J = 3·15
J = 45 anos
Sejam as galinhas representadas pela letra G e as vacas pela letra V, podemos montar as duas equações a seguir:
G + V = 60
2G + 4V = 220
Com essas equações, é possível montar o seguinte sistema, que será resolvido usando o método da substituição.
Observe o valor algébrico de G, na primeira equação:
G + V = 60
G = 60 – V
Substitua esse valor na segunda:
2G + 4V = 220
2(60 – V) + 4V = 220
120 – 2V + 4V = 220
2V = 220 – 120
2V = 100
V = 100
2
V = 50
08/09 - 8º ano EF - ( Matemática ângulos e suas classificações) Parte 1
09/09 - 8º ano EF - ( Matemática ângulos e suas classificações) Parte 2
15/09 - 8º ano EF - Matemática - Mediatriz de um segmento: Parte 4
16/09 - 8º ano EF - Matemática - Mediatriz e bissetriz - Construção de pipas: Parte V
Tipos de Ângulos
Conforme as suas medidas, os ângulos são classificados em agudo, reto, obtuso e raso.
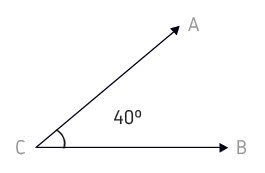
Agudo
O ângulo agudo mede menos do que 90º (
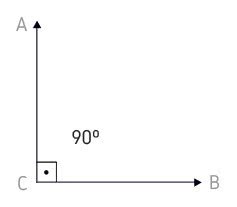
Reto
O ângulo reto mede o mesmo que 90º ( = 90º).
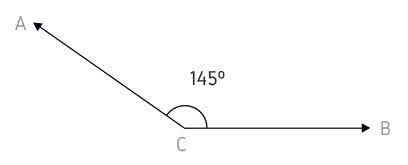
Obtuso
O ângulo obtuso mede mais do que 90º e menos do que 180º (90º >
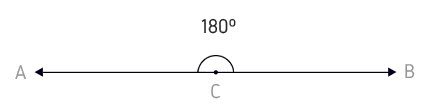
Raso
O ângulo raso, também conhecido como meia volta, mede o mesmo que 180º ( = 180º).
Como medir os ângulos?
Para medir os ângulos, precisamos de um transferidor, um instrumento em círculo (360º) ou semicírculo (180º) que é dividido em graus, e seguir os seguintes passos:
- Colocar o centro da base do transferidor sobre o vértice do ângulo.
- Colocar o ponto que indica 0º do transferidor em um dos lados do ângulo.
- O outro lado do ângulo apontará para a sua medida.
O ângulo é a unidade de medida mais utilizada. Minuto e segundo são os seus múltiplos.
Ângulos Complementares - São aqueles que juntos medem 90º.
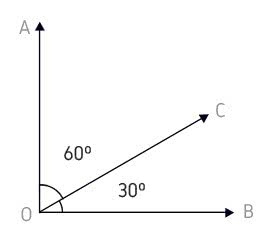
30º + 60º = 90º, o que que dizer que os ângulos se complementam mutuamente, 30º complementa o ângulo de 60º e vice-versa.
Ângulos Suplementares
Ângulos suplementares são aqueles que juntos medem 180º.
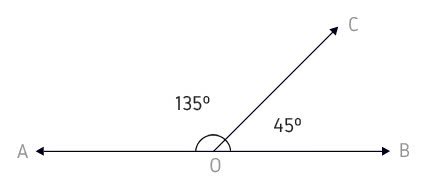
135º + 45º = 180º
Isso quer dizer que o ângulo de 135º é o suplemento do ângulo que mede 45º.
Ao mesmo tempo, o ângulo de 45º é o suplemento do ângulo que mede 135º.
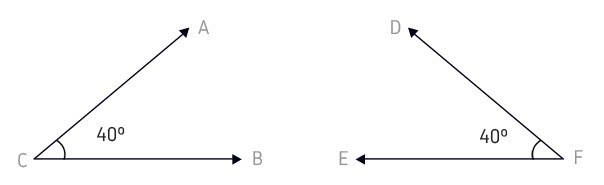
Ângulos Congruentes
Ângulos congruentes são aqueles que têm a mesma medida.
Ângulos Consecutivos
Ângulos consecutivos são aqueles que possuem em comum um lado e um vértice.
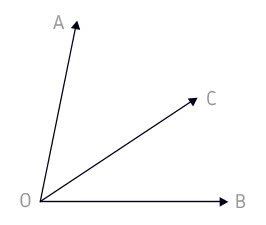
AÔC e CÔB têm em comum o vértice (O) e o lado (OC)
Ângulos Opostos pelo Vértice
Ângulos opostos pelo vértice (OPV) são aqueles cujos lados se opõem aos lados de outro ângulo.
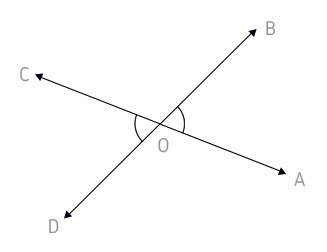
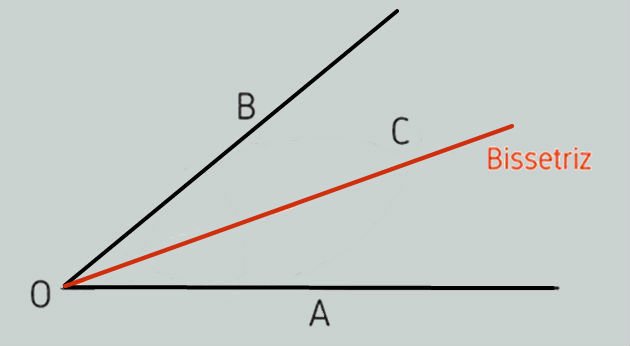
A bissetriz é uma semirreta interna a um ângulo, traçada a partir do seu vértice, e que o divide em dois ângulos congruentes (ângulos com a mesma medida).
Na figura abaixo, a bissetriz, indicada por uma reta em vermelho, reparte o ângulo AÔB ao meio.
Assim, o ângulo AÔB fica dividido em dois outros ângulos, o AÔC e o BÔC, de mesmas medidas.
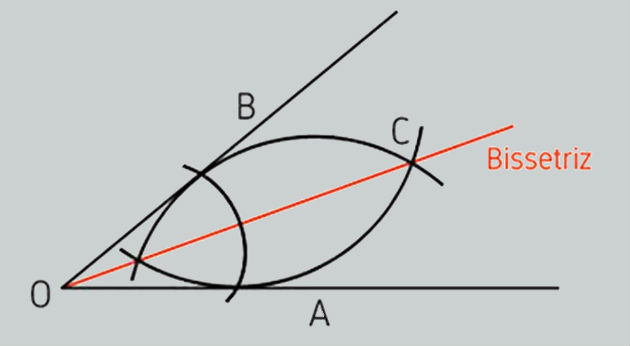
Como encontrar a bissetriz?
Para encontrar a bissetriz, basta seguir os seguintes passos utilizando o compasso:
- abra um pouco o compasso e coloque a sua ponta seca no vértice do ângulo.
- faça um traço de circunferência sobre as semirretas OA e OB.
- com o compasso aberto, coloque a ponta seca no ponto de intersecção da semirreta OA e faça um traço de circunferência com o compasso virado para dentro do ângulo.
- faça o mesmo, agora com a ponta seca no ponto de intersecção da semirreta OB.
- trace uma semirreta do vértice do ângulo até o ponto de intersecção dos traços que acabou de fazer. A semirreta OC é a bissetriz.
Fonte:https://www.todamateria.com.br/bissetriz/
Bissetriz ângulo 30º
Mediatriz
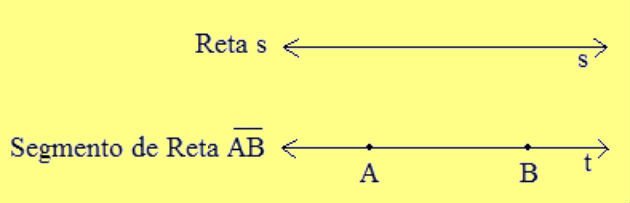
Mediatriz é uma reta perpendicular a um segmento de reta e que passa pelo ponto médio deste segmento.
Todos os pontos pertencentes a mediatriz são equidistantes das extremidades deste segmento.
Lembrando que, diferente da reta, que é infinita, o segmento de reta é limitado por dois pontos de uma reta. Ou seja, ele é considerado uma parte da reta.
Como construir a mediatriz?
Podemos construir a mediatriz de um segmento de reta usando régua e compasso. Para isso, siga os seguintes passos:
- Desenhe um segmento de reta e nas suas extremidades marque o ponto A e o ponto B.
- Pegue um compasso e faça uma abertura que seja um pouco maior que a metade da medida do segmento.
- Com essa abertura, coloque a ponta seca do compasso no ponto A e trace um semicírculo. Permanecendo com a mesma abertura no compasso, faça a mesma coisa no ponto B.
- Os semicírculos traçados se cruzaram em dois pontos, um acima do segmento de reta e outro abaixo. Com a régua, una esses dois pontos, essa reta traçada é a mediatriz do segmento AB.
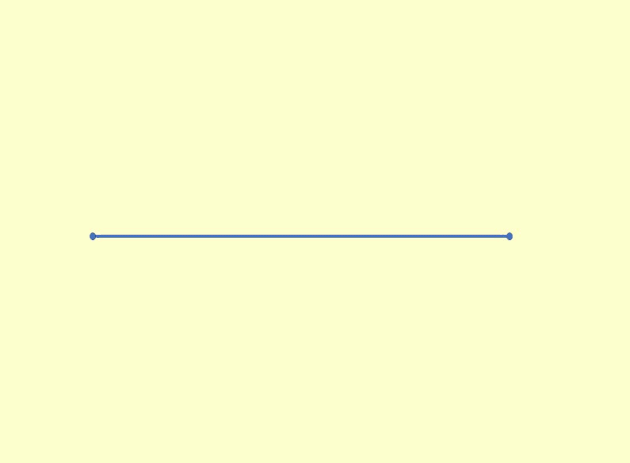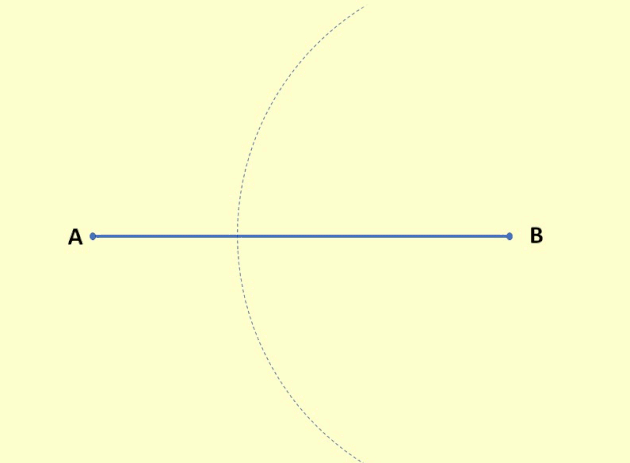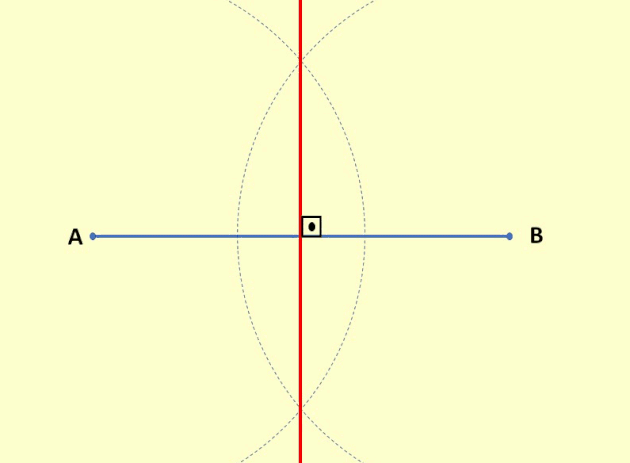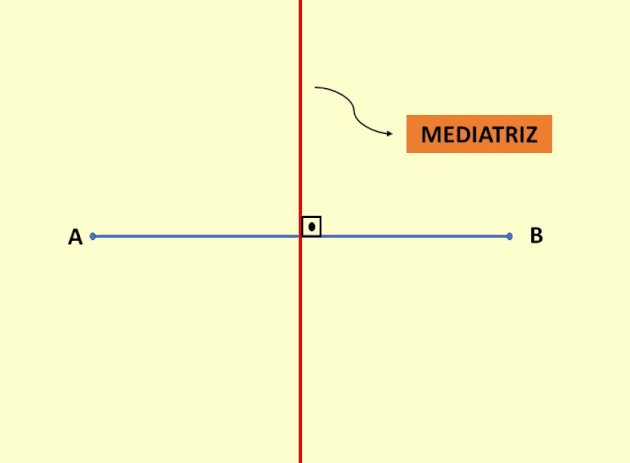







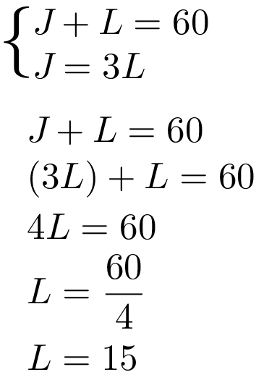

Nenhum comentário:
Postar um comentário